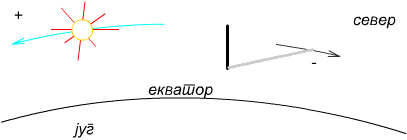Тригонометријске функције

Тригонометријске функције су функције угла. Добиле су име по грани математике која их користи за решавање троуглова, а која се назива тригонометрија.

Када је угао, дакле аргумент ових функција реалан број, тада су то функције равнинске тригонометрије: синус и косинус, од којих се изводе све остале. Од осталих основних функција угла често су у употреби тангенс, па и котангенс, затим, мало ређе се срећу косеканс и секанс, и коначно најређе синус версус и косинус версус. Када је угао комплексан број тада функције угла могу прећи у хиперболичке функције.

Инверзне тригонометријске функције зову се циклометријске функције и аркус-функције, тј. функција^-1.

Дефиниције

Сл.1. Тригонометријски троугао

Основне тригонометријске функције синус, косинус и тангенс се обично дефинишу помоћу правоуглог троугла, слика десно.

$x=r\cdot \cos \varphi ,y=r\cdot \sin \varphi ,\frac{y}{x}=\mathrm{tg}\varphi .$

Позитиван математички угао има супротан смер од казаљке на сату, слично као и кретање Сунца у односу на сунчеву сенку на слици 2.

Тригонометријска кружница

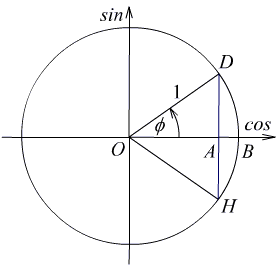
На слици (3) доле је кружница полупречника један са центром у исходишту, тј. $x^2+y^2=1,$ која се зове тригонометријска кружница.

У следећој дефиницији и теореми (1), тангенс и котангенс (б) се у англосаксонским земљама означавају tan и cot, косеканс (в) се и код нас означава cosec.

Сл.3. Тригонометријска кружница

Дефиниција 1

Тригонометријске реалне функције угла φ дефинишу се једнакостима

(а) ${\cos }^2\varphi +{\sin }^2\varphi =1,$ синус и косинус су реални бројеви;

(б) $\mathrm{tg}\varphi =\frac{\sin \varphi }{\cos \varphi },\mathrm{ctg}\varphi =\frac{\cos \varphi }{\sin \varphi },$ тангенс и котангенс;

(в) $\sec \varphi =\frac{1}{\cos \varphi },\csc \varphi =\frac{1}{\sin \varphi },$ секанс и косеканс.

(г) $\mathrm{vercos}\varphi =1-\sin \varphi ,\mathrm{versin}=1-\cos \varphi ,$ косинус версус и синус версус.

Функције (в), а нарочито (г) ретко срећемо.

Теорема 1

(а) $\overline{OA}=\cos \varphi ,\overline{OC}=\sin \varphi ,$ косинус и синус;

(б) $\overline{BE}=\mathrm{tg}\varphi ,\overline{FG}=\mathrm{ctg}\varphi ,$ тангенс и котангенс;

(в) $\overline{OE}=\sec \varphi ,\overline{OG}=\csc \varphi ,$ секанс и косеканс.

Доказ

Тачка Т са слике 1. овде (сл.2.) је тачка D.

(а) Следи непосредно због полупречника r = 1.

(б) Уочимо сличне троуглове $\mathrm{\Delta }EBO\sim \mathrm{\Delta }DAO,$ одакле $\overline{BE}:\overline{OB}=\overline{AD}:\overline{OA},$ тј. $\overline{BE}:1=\sin \varphi :\cos \varphi ;$ уочимо сличне троуглове $\mathrm{\Delta }GFO\sim \mathrm{\Delta }OAD,$ одатле $\overline{FG}:\overline{FO}=\overline{OA}:\overline{AD},$ тј. $\overline{FG}:1=\cos \varphi :\sin \varphi .$

(в) Из истих сличних троуглова (б) добијамо $\overline{OE}:\overline{OB}=\overline{OD}:\overline{OA},$ тј. $\overline{OE}:1=1:\cos \varphi ;$ затим $\overline{OG}:\overline{OF}=\overline{OD}:\overline{AD},$ тј. $\overline{OG}:1=1:\sin \varphi .$

Крај доказа.

Посебни углови

Овде ће бити анализиране особине вредности тригонометријских функција за посебне углове.

Предзнак

На претходној слици (3) представљен је Декартов правоугли систем координата и тачка D на тригонометријској кружници. Угао BOD = φ може неограничено расти док покретни крак угла (OD) пролази редом кроз први, други, трећи и четврти квадрант, а затим поново по истом кругу. Дакле, угао φ може расти до 360° и даље. При томе се пројекције тачке D на апсцису и ординату увек рачунају као косинус и синус угла φ. То значи да је косинус позитиван када је тачка -{D}- у првом и четвртом квадранту, а да је синус позитиван када је тачка -{D}- у првом и другом квадранту. Детаљно то видимо у следећој табели:

Тригонометријске функције по квадрантима

Квадрант	1. (0°-90°)	2. (90°-180°)	3. (180°-270°)	4. (270°-360°)
синус	+	+	-	-
косинус	+	-	-	+
тангенс	+	-	+	-

Свођење на први квадрант

Лако је преко тригонометријске кружнице или адиционих формула проверити тачност формула за свођење вредности тригонометријских функција на функције углова из првог квадранта:

$\cos (180^o-\varphi )=-\cos \varphi ,\sin (180^o-\varphi )=\sin \varphi ,$

$\cos (180^o+\varphi )=-\cos \varphi ,\sin (180^o+\varphi )=-\sin \varphi ,$

$\cos (-\varphi )=\cos \varphi ,\sin (-\varphi )=-\sin \varphi .$

Функције косинус и синус су периодичне са основним периодом 360°, a функција тангенс је периодична са периодом 180°:

$\cos (360^o+\varphi )=\cos \varphi ,\sin (360^o+\varphi )=\sin \varphi ,\mathrm{tg}(180^o+\varphi )=\mathrm{tg}\varphi .$

Период синусне и косинусне функције може се наћи из формуле: $T=\frac{2\pi }{\omega }$

Тако је период функције $\sin 2\alpha$ једнак $T=\frac{2\pi }{2}$, односно $\pi$.

Функције углове већих од 360 степени претходним формулама се своде на функције мањих углова, а затим даље, ако је потребно, на први квадрант, на начин видљив у следећој табели:

$\beta$	$\frac{\pi }{2}+\alpha$	$\pi +\alpha$	$\frac{3\pi }{2}+\alpha$	$\frac{\pi }{2}-\alpha$	$\pi -\alpha$	$\frac{3\pi }{2}-\alpha$	$2\pi -\alpha$
$\sin \beta$	$\cos \alpha$	$-\sin \alpha$	$-\cos \alpha$	$\cos \alpha$	$\sin \alpha$	$-\cos \alpha$	$-\sin \alpha$
$\cos \beta$	$-\sin \alpha$	$-\cos \alpha$	$\sin \alpha$	$\sin \alpha$	$-\cos \alpha$	$-\sin \alpha$	$\cos \alpha$
$\mathrm{tg}\beta$	$-\mathrm{ctg}\alpha$	$\mathrm{tg}\alpha$	$-\mathrm{ctg}\alpha$	$\mathrm{ctg}\alpha$	$-\mathrm{tg}\alpha$	$\mathrm{ctg}\alpha$	$\mathrm{tg}\alpha$
$\mathrm{ctg}\beta$	$-\mathrm{tg}\alpha$	$\mathrm{ctg}\alpha$	$-\mathrm{tg}\alpha$	$\mathrm{tg}\alpha$	$-\mathrm{ctg}\alpha$	$\mathrm{tg}\alpha$	$\mathrm{ctg}\alpha$

У општем случају то се може записати овако:

$f(n\pi +\alpha )=\pm f(\alpha )$

$f(n\pi -\alpha )=\pm f(\alpha )$

$f(\frac{(2n+1)\pi }{2}+\alpha )=\pm g(\alpha )$

$f(\frac{(2n+1)\pi }{2}-\alpha )=\pm g(\alpha )$

Притом је f — произвољна тригонометријска функција, g — одговарајућа јој функција (косинус за синуса, синус за косинус и аналогно за остале функције), а n — цео број.

Вредности тригонометријских функција

Вредности тригонометријских функција приказане на тригонометријској кружници

За неке од углова из првог квадранта се функције лакше израчунавају:

Најчешће вредности тригонометријских функција

$\varphi$	0°	30°	45°	60°	90°
$\sin \varphi$	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
$\cos \varphi$	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
$\mathrm{tg}\varphi$	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	$\pm \mathrm{\infty }$

Један од начина израчунавања ових вредности је приказан у прегледу основних углова. Из табеле се види да су већ код „основних“ углова тригонометријске функције ирационални бројеви и да би слични изрази за друге углове могли бити још сложенији. Једноставнији од тих сложенијих израза био би, на пример $\sin 15^o=\frac{\sqrt{3}-1}{2\sqrt{2}},$ и то је најмањи угао чији се синус може представити писањем просте алгебарске комбинације рационалних бројева и коренова. Вековима су тригонометријске вредности записиване у тригонометријске таблице, на 5 до 10 децимала, a у последње време користи се скоро искључиво рачунар или калкулатор.

Вредности тригонометријских функција неких углова које се нешто дужим путем израчунавају дати су у следећој табели:

$\alpha$	$\frac{\pi }{12}=15^{\circ }$	$\frac{\pi }{10}=18^{\circ }$	$\frac{\pi }{8}=22.5^{\circ }$	$\frac{\pi }{5}=36^{\circ }$	$\frac{3\pi }{10}=54^{\circ }$	$\frac{3\pi }{8}=67.5^{\circ }$	$\frac{2\pi }{5}=72^{\circ }$
$\sin \alpha$	$\frac{\sqrt{3}-1}{2\sqrt{2}}$	$\frac{\sqrt{5}-1}{4}$	$\frac{\sqrt{2-\sqrt{2}}}{2}$	$\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}$	$\frac{\sqrt{5}+1}{4}$	$\frac{\sqrt{2+\sqrt{2}}}{2}$	$\frac{\sqrt{5+\sqrt{5}}}{2\sqrt{2}}$
$\cos \alpha$	$\frac{\sqrt{3}+1}{2\sqrt{2}}$	$\frac{\sqrt{5+\sqrt{5}}}{2\sqrt{2}}$	$\frac{\sqrt{2+\sqrt{2}}}{2}$	$\frac{\sqrt{5}+1}{4}$	$\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}$	$\frac{\sqrt{2-\sqrt{2}}}{2}$	$\frac{\sqrt{5}-1}{4}$
$\mathrm{tg}\alpha$	$2-\sqrt{3}$	$\sqrt{1-\frac{2}{\sqrt{5}}}$	$\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}$	$\sqrt{5-2\sqrt{5}}$	$\sqrt{1+\frac{2}{\sqrt{5}}}$	$\sqrt{\frac{\sqrt{2}+1}{\sqrt{2}-1}}$	$\sqrt{5+2\sqrt{5}}$
$\mathrm{ctg}\alpha$	$2+\sqrt{3}$	$\sqrt{5+2\sqrt{5}}$	$\sqrt{\frac{\sqrt{2}+1}{\sqrt{2}-1}}$	$\sqrt{1+\frac{2}{\sqrt{5}}}$	$\sqrt{5-2\sqrt{5}}$	$\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}$	$\sqrt{1-\frac{2}{\sqrt{5}}}$

Када тачка -{D}- једном обиђе кружницу пређе пут 2π односно направи 360°. Лук дужине π одговара углу 180° - испружени угао, π/2 је 90° - прави угао, π/3 је 60°, π/4 је 45°, π/6 је 30°, и уопште лук дужине x радијана одговара углу 360x/2π степени. За један радијан, х = 1, добија се угао 57,2957795... степени, тј. у степенима, минутима и секундама 57°17'44,8". Један степен има 60 минута, а једна минута има 60 секунди. Изрази минуте и секунде потичу од латинских речи: -{partes minutae primae}- и -{partes minutae secundae}-, тј. први мали делови и други мали делови. Математички текстови за јединицу угла подразумевају радијан.

Редови

Тригонометријске функције се, такође, могу представљати (бесконачним) редовима:

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{x}^{2n+1}}{(2n+1)!}$

$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...==\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{x}^{2n}}{(2n)!}$

Ови редови се могу употребити и за дефинисање тригонометријских функција комплексног броја z, и хиперболичких функција.

Имајући у виду једнакости $\mathrm{tg}x=\frac{\sin x}{\cos x},$ $\mathrm{ctg}x=\frac{\cos x}{\sin x},$ $\sec x=\frac{1}{\cos x}$ и $\mathrm{cosec}x=\frac{1}{\sin x},$ у Тејлоров ред се могу разложити следеће функције:

$\mathrm{tg}x=x+\frac{1}{3}{x}^3+\frac{2}{15}{x}^5+\frac{17}{315}{x}^7+\frac{62}{2835}{x}^9+\cdots =\sum _{n=1}^{\mathrm{\infty }}\frac{2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}{x}^{2n-1}(-\frac{\pi }{2}<x<\frac{\pi }{2}),$

$\mathrm{ctg}x=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\frac{2x^5}{945}-\frac{x^7}{4725}-\cdots =\frac{1}{x}+\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n{2}^{2n}|B_{2n}|}{(2n)!}{x}^{2n-1}(-\pi <x<\pi ),$

$\sec x=1+\frac{1}{2}{x}^2+\frac{5}{24}{x}^4+\frac{61}{720}{x}^6+\frac{277}{8064}{x}^8+\cdots =1+\sum _{n=1}^{\mathrm{\infty }}\frac{E_n}{(2n)!}{x}^{2n},(-\frac{\pi }{2}<x<\frac{\pi }{2}),$

$\csc x=\frac{1}{x}+\frac{1}{6}x+\frac{7}{360}{x}^3+\frac{31}{15120}{x}^5+\frac{127}{604800}{x}^7+\cdots =\frac{1}{x}+\sum _{n=1}^{\mathrm{\infty }}\frac{2(2^{2n-1}-1)B_n}{(2n)!}{x}^{2n-1}(-\pi <x<\pi ),$

Графици

Тригонометријске функције се могу графички представити. На следећим сликама су приказани њихови графици:

Графици тригонометријских функција: синуса, косинуса, тангенса, секанса, косеканса, котангенса

Парност

Косинус и секанс су парне функције, док су преостале четири непарне функције:

$\sin (-\alpha )=-\sin \alpha ,$

$\cos (-\alpha )=\cos \alpha ,$

$\mathrm{t}\mathrm{g}(-\alpha )=-\mathrm{t}\mathrm{g}\alpha ,$

$\mathrm{c}\mathrm{t}\mathrm{g}(-\alpha )=-\mathrm{c}\mathrm{t}\mathrm{g}\alpha ,$

$\sec (-\alpha )=\sec \alpha ,$

$\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{c}(-\alpha )=-\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{c}\alpha .$

Гранична вредност

Сл.4. Тетива је краћа од лука

На слици (4) лево видимо тетиву

$\overline{DAH}$

која је сигурно краћа од лука

$\widehat{DBH}.$

Тетива је најкраће растојање између две тачке на кружници. Зато је полутетива

$\overline{DA}$

краћа од полулука

$\widehat{DB}.$

Троугао OAD, са оштрим углом φ је правоугли. Прави угао је у темену А, катета ОА износи

$\cos \varphi$

, катета DA износи

$\sin \varphi$

, хипотенуза је дужине један. Када је угао у радијанима и

$0<\varphi <\frac{\pi }{2},$

тада је

Теорема 1

$\underset{\varphi \to 0}{\lim }\sin \varphi =0,\underset{\varphi \to 0}{\lim }\cos \varphi =1.$

Доказ: Следи из $0<\sin \varphi <\widehat{DB}=\varphi$ и $0<1-\cos \varphi <\overline{AB}<\overline{DB}<\widehat{DB}=\varphi .$ Крај.

Када угао тежи нули преко позитивних вредности, синус је тада позитиван, а негативан је када угао тежи нули преко негативних вредности. Напротив, косинус је у оба случаја позитиван. Из тога произилазе лимеси за котангенс: $\underset{x\to +0}{\lim }\mathrm{ctg}x=+\mathrm{\infty },\underset{x\to -0}{\lim }\mathrm{ctg}x=-\mathrm{\infty }.$ Заменом х са комплементним углом добићете одговарајуће лимесе за тангенс.

Сл.5. Тригонометријски круг

Теорема 2

$\underset{x\to 0}{\lim }\frac{\sin x}{x}=1.$

Доказ

На слици (5) десно, површина правоуглог троугла OAD мања је од површине кружног исечка OBD, а ова опет мања од површине правоуглог троугла OBE. Назовимо са х угао BOE. Отуда $\frac{\sin x\cos x}{2}<\frac{x}{2}<\frac{\mathrm{tg}x}{2}.$ Поделимо ли ове неједнакости са (позитивним) $\frac{\sin x}{2},$ добићемо $\cos x<\frac{x}{\sin x}<\frac{1}{\cos x},$ а отуда $\frac{1}{\cos x}>\frac{\sin x}{x}>\cos x.$ Са $x\to 0$ вреди $\cos x\to 1,\frac{1}{\cos x}\to 1,$ па је $\frac{\sin x}{x}\to 1.$ Синус је парна функција па је доказ за негативне углове исти. Крај доказа.

Извод

Извод функције f(x) по дефиницији је гранична вредност: $f^{\prime }(x)=\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{\mathrm{\Delta }f(x)}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}.$

Теорема 3

(а) $(\sin x{)}^{\prime }=\cos x,$

(б) $(\cos x{)}^{\prime }=-\sin x,$

(в) $(\mathrm{tg}x{)}^{\prime }={\sec }^{2}x.$

(г) $(\mathrm{ctg}x{)}^{\prime }=-{\csc }^{2}x.$

Доказ

(а) $\mathrm{\Delta }\sin x=\sin (x+\mathrm{\Delta }x)-\sin x=2\cos (x+\frac{\mathrm{\Delta }x}{2})\sin \frac{\mathrm{\Delta }x}{2},$ па је

$\frac{\mathrm{\Delta }\sin x}{\mathrm{\Delta }x}=\frac{\cos (x+\frac{\mathrm{\Delta }x}{2})}{\frac{\mathrm{\Delta }x}{2}}\to \cos x,$ када $\mathrm{\Delta }x\to 0$ (теорема 2).

(б) Због $\cos x=\sin (\frac{\pi }{2}-x),$ биће $(\cos x{)}^{\prime }=\cos (\frac{\pi }{2}-x)\cdot (\frac{\pi }{2}-x{)}^{\prime }=-\cos (\frac{\pi }{2}-x)=-\sin x.$

(в) Извод количника $(\mathrm{tg}x{)}^{\prime }=\left(\frac{\sin x}{\cos x}\right)=$

$=\frac{{\sin }^{\prime }x\cos x-{\cos }^{\prime }x\sin x}{{\cos }^{2}x}=\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}=\frac{1}{{\cos }^{2}x}={\sec }^{2}x.$

(г) Извод количника $(\mathrm{ctg}x{)}^{\prime }=\left(\frac{\cos x}{\sin x}\right)=$

$=\frac{{\cos }^{\prime }x\sin x-{\sin }^{\prime }x\cos x}{{\sin }^{2}x}=\frac{-{\sin }^{2}x-{\cos }^{2}x}{{\sin }^{2}x}=-\frac{1}{{\sin }^{2}x}=-{\csc }^{2}x.$ Крај доказа 3.

Интеграли тригонометријских функција

Шаблон:Посебан чланак Интеграли неких тригонометријских функција приказани су овде:

$f(x)$	$f^{\prime }(x)$	$\int f(x)dx$
$\sin x$	$\cos x$	$-\cos x+C$
$\cos x$	$-\sin x$	$\sin x+C$
$\tan x$	${\sec }^{2}x=1+{\tan }^{2}x$	$-\ln |\cos x|+C$
$\cot x$	$-{\csc }^{2}x=-(1+{\cot }^{2}x)$	$\ln |\sin x|+C$
$\sec x$	$\sec x\tan x$	$\ln |\sec x+\tan x|+C$
$\csc x$	$-\csc x\cot x$	$-\ln |\csc x+\cot x|+C$

Друге особине

Преглед скоро свих особина тригонометријских функција које се тичу решавања троуглова дат је у прилогу: равнинска тригонометрија.

У посебном прилогу могу се пронаћи докази за адиционе формуле, где спадају и формуле за двоструке углове, затим половине углова, те представљање збира и разлике тригонометријских функција помоћу производа и обратно, и изражавање осталих тригонометријских функција помоћу тангенса половине угла.

Такође, у посебном прилогу се налазе тригонометријске једначине.

Тригонометријске функције као решења диференцијалних једначина

Тригонометријске функције косинус и синус могу се представити као решења диференцијалне једначине:

$\frac{d^2}{d{\phi }^2}R(\phi )=-R(\phi ),$

са почетним условом $\cos (0)={\sin }^{\prime }(0)=1$.

${\cos }^{″}x=-\cos x,$

${\sin }^{″}x=-\sin x.$

Тригонометријске функције као решења функционалних једначина

Функције косинус и синус се могу одредити као непрекидна решења система функционалних једначина:

$\{\begin{array}{ccc}f(x+y)& =& f(x)f(y)-g(x)g(y)\\ g(x+y)& =& g(x)f(y)+f(x)g(y)\end{array}$

Инверзне тригонометријске функције

Шаблон:Посебан чланак Инверзне тригонометријске функције су -{arcsin}- x (аркус синус икс), -{arccos}- x (аркус косинус), -{arctg}- x (аркус тангенс), -{arcctg}- x (аркус котангенс). Оне су инверзне тригонометријским функцијама -{sin}- x (синус икс), -{cos}- x (косинус), -{tg}- x (тангенс), -{ctg}- x (котангенс). Префикс аркус потиче од латинске речи -{arcus}- - лук, угао. Називају се још и циклометријским функцијама.

$\begin{array}{ccccc}\text{za}& -\frac{\pi }{2}\le y\le \frac{\pi }{2},& y=\arcsin x& \text{ako}& x=\sin y;\\ \\ \text{za}& 0\le y\le \pi ,& y=\arccos x& \text{ako}& x=\cos y;\\ \\ \text{za}& -\frac{\pi }{2}<y<\frac{\pi }{2},& y=\arctan x& \text{ako}& x=\tan y;\\ \\ \text{za}& -\frac{\pi }{2}\le y\le \frac{\pi }{2},y\ne 0,& y=\mathrm{arccsc}x& \text{ako}& x=\csc y;\\ \\ \text{za}& 0\le y\le \pi ,y\ne \frac{\pi }{2},& y=\mathrm{arcsec}x& \text{ako}& x=\sec y;\\ \\ \text{za}& 0<y<\pi ,& y=\mathrm{arccot}x& \text{ako}& x=\cot y.\end{array}$

Примена у физици

Примена тригонометрије и тригонометријских функција у физици је јако велика.

Тако се на пример прилично користе у анализи простирања таласа, описивању хармонијских осцилација као периодичног кретања, представљања наизменичне струје итд.

Види још

• Тригонометријске једначине
• Раванска тригонометрија
• Функција
• Списак интеграла тригонометријских функција
• Инверзне тригонометријске функције