Радијан

Лук круга исте дужине као и полупречник тог круга обухвата угао од 1 радијана. Обим обухвата угао од 2Шаблон:Math радијана.

У математици и физици, радијан је мерна јединица угла. То је СИ изведена јединица за угао. Дефинисана је као угао код центра круга затворен луком кружнице који је једнак у дужини полупречнику круга. Мере угла у радијанима су често дате без икакве експлицитне јединице. Када се да јединица, користи се скраћеница rad, а понекад симбол ^c (за циркуларни).

Дефиниција

Потпуна револуција је 2Шаблон:Pi радијана (овде је приказана кругом полупречника један, а тиме и обимом 2Шаблон:Pi).

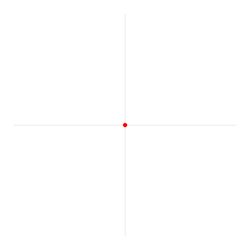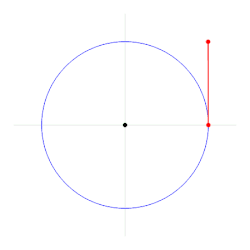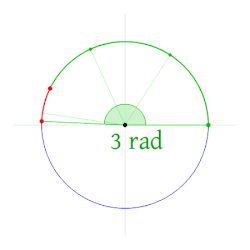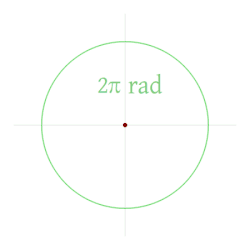
Један радијан се дефинише као угао формиран од центра круга који пресеца лук једнаке дужине полупречнику круга. Уопштеније, магнитуда тог угла у радијанима једнака је односу дужине лука и полупречника круга; то јест, Шаблон:Math, где је Шаблон:Mvar угао у радијанима, Шаблон:Mvar је дужина лука, а Шаблон:Mvar је полупречник. Супротно томе, дужина пресеченог лука једнака је полупречнику помноженом са величином угла у радијанима; односно Шаблон:Math.

Као однос две дужине, радијан је чист број.Шаблон:Efn У СИ, радијан је дефинисан као да има вредност 1. Као последица тога, у математичком писању, симбол „rad“ се скоро увек изоставља. Када се квантификује угао у одсуству било ког симбола, претпостављају се радијани, а када се мисли на степене, користи се знак степена Шаблон:Char.

Из тога следи да је величина у радијанима једног потпуног обртаја (360 степени) дужина целог обима подељена полупречником, или Шаблон:Math, или 2Шаблон:Pi. Тако је 2Шаблон:Pi радијана једнако 360 степени, што значи да је један радијан једнак 180/Шаблон:Pi ≈ Шаблон:Gaps степени.

Релација Шаблон:Math се може извести коришћењем формуле за дужину лука, ${\ell }_{\text{arc}}=2\pi r\left(\frac{\theta }{360^{\circ }}\right)$, и коришћењем круга полупречника 1. Пошто је радијан мера угла који спаја лук дужине једнаке полупречнику круга, следи $1=2\pi \left(\frac{1\text{ rad}}{360^{\circ }}\right)$. Ово се даље може поједноставити на $1=\frac{2\pi \text{ rad}}{360^{\circ }}$. Множење обе стране са 360° даје Шаблон:Math.

Историја

Концепт радијанске мере, за разлику од степена угла, обично се приписује Роџеру Котсу 1714. године. Он је описао радијан у свему осим у имену и препознао његову природност као јединицу угаоне мере. Пре него што је термин радијан постао широко распрострањен, јединица се обично звала кружна мера угла.

Идеју о мерењу углова дужином лука већ су користили други математичари. На пример, ал-Каши (око 1400) користио је такозване делове пречника као јединице, где је један део пречника био Шаблон:Sfrac радијана. Такође су користили сексагезималне подјединице дела пречника.

Термин радијан се први пут појавио у штампи 5. јуна 1873. у испитним питањима које је поставио Џејмс Томсон (брат лорда Келвина) на Квинс колеџу у Белфасту. Он је користио тај термин још 1871. године, док је 1869. Томас Мјур, тада са Универзитета Сент Ендруз, колебао између појмова -{rad}-, -{radial}-, и -{radian}-. Године 1874, након консултација са Џејмсом Томсоном, Мјур је усвојио радијан. Име радијан није било универзално усвојено неко време након овога. Лонгмансова школска тригонометрија је и користила назив радијанска кружна мера када је објављена 1890.

Симбол јединице

Међународни биро за тегове и мере и Међународна организација за стандардизацију наводе -{rad}- као симбол радијана. Алтернативни симболи који су коришћени пре 100 година су ^-{c}- (наднасловно написано слово -{c}-, за „кружну меру“), слово -{r}- или суперскрипт Шаблон:Sup, али се ове варијанте ретко користе, јер могу бити помешане са симболом степена (°) или полупречником (-{r}-). Стога би вредност од 1,2 радијана најчешће била записана као 1,2 rad; друге ознаке укључују 1,2 r, 1,2Шаблон:Sup, 1,2Шаблон:Sup, или 1,2Шаблон:Sup.

Конверзије

Постоје 2π (око 6,283185) радијана у пуном кругу, па:

2π rad = 360°
1 rad = 360°/2π = 180°/π (приближно 57,29578°).

или:

$360^{\circ }=2\pi \text{rad}$

$1^{\circ }=\frac{2\pi }{360}\text{rad}=\frac{\pi }{180}\text{rad}$

У математичкој анализи, углови морају да се представе у радијанима у тригонометријским функцијама, да би идентитети и резултати били што простији и природнији. На пример, употреба радијана води до простог идентитета

$\underset{h\to 0}{\lim }\frac{\sin h}{h}=1$,

који је основа за многе друге елегантне идентитете у математици, укључујући

$\frac{d\sin x}{dx}=\cos x$.

Радијан је пре био СИ допунска јединица, али је ова категорија укинута из СИ система 1995. године.

Треба нагласити да, иако је радијан јединица за меру, све мерено у радијанима је бездимензионално. Ово може лако да се уочи у томе да је однос дужине лука и полупречника у ствари угао лука, мерен у радијанима; а ипак количник два растојања је без димензија. Величине углова су напросто бројеви—у математичком смислу—а не физичке величине мерене у односу на известан фиксан еталон. Величина угла, у радијанима, степенима или ма којој другој јединици, независна је од јединице која се користи за изражавање дужина и других физичких мерљивих величина.

За мерење просторних углова, видите стерадијан.

Предности мерења у радијанима

Неки уобичајени углови, мерени у радијанима. Сви велики полигони у овом дијаграму су правилни полигони.

У калкулусу и већини других грана математике изван практичне геометрије, углови се универзално мере у радијанима. То је зато што радијани имају математичку „природности” која доводи до елегантније формулације бројних важних резултата. Што је најважније, резултати у анализи која укључује тригонометријске функције могу се елегантно навести, када су аргументи функција изражени у радијанима. На пример, употреба радијана доводи до једноставне формуле лимита

$\underset{h\to 0}{\lim }\frac{\sin h}{h}=1,$

што је основа многих других идентитета у математици, укључујући

$\frac{d}{dx}\sin x=\cos x$

$\frac{d^2}{d{x}^2}\sin x=-\sin x.$

Због ових и других својстава, тригонометријске функције се појављују у решењима математичких проблема који нису очигледно повезани са геометријским значењима функција (на пример, решења диференцијалне једначине: $\frac{d^{2}y}{d{x}^2}=-y$, израчунавања интеграла $\int \frac{dx}{1+x^2},$ и тако даље). У свим таквим случајевима, нађено је да су аргументи функција најприродније написани у облику који одговара, у геометријском контексту, радијанском мерењу углова.

Тригонометријске функције такође имају једноставна и елегантна проширења серије када се користе радијани. На пример, када је x у радијанима, Тејлоров низ за -{sin x}- постаје:

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots .$

Ако је x изражено у степенима, онда би серија садржала непрегледне факторе који укључују степене Шаблон:Pi/180: ако је x број степени, број радијана је Шаблон:Nowrap, тако да

$\sin x_{\mathrm{d}\mathrm{e}\mathrm{g}}=\sin y_{\mathrm{r}\mathrm{a}\mathrm{d}}=\frac{\pi }{180}x-{\left(\frac{\pi }{180}\right)}^3\frac{x^3}{3!}+{\left(\frac{\pi }{180}\right)}^5\frac{x^5}{5!}-{\left(\frac{\pi }{180}\right)}^7\frac{x^7}{7!}+\cdots .$

У сличном духу, математички важни односи између синусних и косинусних функција и експоненцијалне функције (погледајте, на пример, Ојлерову формулу) могу се елегантно изразити, када су аргументи функција у радијанима (а иначе неуредни).

Димензионална анализа

Иако је радијан јединица мере, он је бездимензионална величина. Ово се може видети из раније дате дефиниције: угао везан за центар круга, мерен у радијанима, једнак је односу дужине затвореног лука и дужине полупречника круга. Пошто се мерне јединице поништавају, овај однос је бездимензионалан.

Иако поларне и сферне координате користе радијане за описивање координата у две и три димензије, јединица се изводи из радијусне координате, тако да је мера угла и даље бездимензионална.

Види још

• Тригонометрија
• Хармонијска анализа
• Угаона фреквенција
• Степени
• Пи

Литература

• Шаблон:GreenBook3rd
• Шаблон:GreenBook2nd