Комплексан број

Комплексни број може бити визуелно представљени као пар бројева Шаблон:Math који формирају вектор на дијаграму који се назива Аргандов дијаграм, чиме се представља комплексна раван. -{„Re“}- је реална оса, -{„Im“}- је имагинарна оса, и Шаблон:Math је имагинарна јединица која задовољава Шаблон:Math.

Уређени пар реалних бројева, означен са $(a,b)$, при чему су $a$ и $b$ реални бројеви ($a,b\in ℝ$), назива се комплексан број. (Реалан број је „прост“, док је уређени пар „сложен“, или комплексан, јер га сачињавају два броја). Скуп свих оваквих парова, односно свих комплексних бројева, означавамо са $ℂ$ и он је суштински Декартов производ $ℂ=ℝ\times ℝ$. Уређени пар $(a,b)$, као комплексан број, записује се још као $a+bi$. Притом се елемент $i$ назива имагинарна јединица, и има својство да је $i^2=-1$. Шаблон:Sfn Имагинарни број се у физици често обележава и латиничним словом $j$.

У скупу комплексних бројева могуће је вршити операције сабирања, множења и дељења и оне се дефинишу на следећи начин:

$(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$ (сабирамо први са првим, други са другим)

$(x_1,y_1)\cdot (x_2,y_2)=(x_1{x}_2-y_1{y}_2,x_1{y}_2+x_2{y}_1)$ (до овог резултата је лако доћи ако их помножимо у облику $(x_1+y_{1}i)\cdot (x_2+y_{2}i)$ и запамтимо да је $i^2=-1$)

$\frac{(x_1,y_1)}{(x_2,y_2)}=(\frac{x_1{x}_2+y_1{y}_2}{x_2^2+y_2^2},\frac{x_2{y}_1-x_1{y}_2}{x_2^2+y_2^2})$ (применимо методу као код множења, с тим што израз у имениоцу помножимо са $x_2-y_{2}i$)

У комплексном броју $z=a+bi$ број $a$ се назива реални део и пише се $a=Re(z)$, а број $b$ је имагинарни део и пише се $b=Im(z)$.

Комплексан број чији је реални део једнак нули назива се чисто имагинарни број.

Скуп реалних бројева може се посматрати као подскуп скупа комплексних бројева (кад је други члан уређеног пара, односно коефицијент уз $i$, једнак нули). Иако се комплексним бројевима не изражавају количине, као што је то случај с реалним бројевима, њихово увођење се користи у решавању проблема састављених у терминима реалних бројева, на пример, проблема о пролазу струје кроз проводник, о профилу крила авиона (користећи функције Жуковског), итд.

Није мање важна ни примена комплексних бројева на чисто математичке проблеме. Тако на пример, за налажење корена кубне једначине потребне су операције с комплексним бројевима. Историјски, комплексни бројеви су уведени због решавања квадратних једначина. Свака квадратна једначина облика $a{x}^2+bx+c=0$ има два решења у скупу комплексних бројева, док смо у скупу реалних бројева наилазили на проблем кад је у решењу облика $x=(-b\pm \sqrt{b^2-4ac})/2a$ израз испод корена био негативан. Увођењем имагинарног броја са својством да је $i^2=-1$, корен поприма облик $\sqrt{i^2|b^2-4ac|}=\sqrt{i^2}\sqrt{|b^2-4ac|}=i\sqrt{b^2-4ac}$ и решење добијамо у скупу комплексних бројева. Чињеница да комплексни бројеви не изражавају величине дала је повод за идеалистичко тумачење комплексних бројева (Г. Лајбниц). велика заслуга у смислу материјалистичког тумачења комплексних бројева припада Л. Ојлеру. Комплексни број се аксиоматски дефинише као уређен пар реалних бројева $(a,b)$. Формуле сабирања, множења, дељења се постулирају овако:

$(a,b)+(x,y)=(a+x,b+y)$, $(a,b)\cdot (x,y)=(ax-by,ay+bx)$, $\frac{(a,b)}{(x,y)}=(\frac{ax+by}{x^2+y^2},\frac{bx-ay}{x^2+y^2})$.

Пар $(0;1)$ се назива имагинарна јединица и означава симболом $i$. Из последњих формула произилази да је $i^2=-1$. Операције са комплексним бројевима задовољавају обичне законе комутативности, дистрибутивности и асоцијативности (као и у случају реалних бројева). Међутим, операције с комплексним бројевима под радикалима (коренима) донекле се разликују од аналогних операција с реалним бројевима. Тако је

$-1=i^2=\sqrt{-1}\cdot \sqrt{-1}=\sqrt{(-1)(-1)}=1$.

Дефиниција

Дефиницију комплексних бројева као уређених парова дао је Вилијам Р. Хамилтон, ирски математичар (1805– 1865) Та се дефиниција темељи само на особини реалних бројева, чиме се избјегава донекле неразјашњени појам броја $\sqrt{-1}$ .

С друге стране, запис облика $z=x+yi$ погоднији је за рачунање.

Оба облика комплексног броја

$z=x+yi$ i

$z=(x,y)$ потпуно су еквивалентна.

Скуп комплексних бројева $ℂ$ је скуп свих бројева облика $z=x+iy$, где су $x,y\in ℝ$.

Посебно је $0=0+i0$.

$x=\mathrm{R}\mathrm{e}(z)$ је реални део комплексног броја $z$,

$y=\mathrm{I}\mathrm{m}z$ је имагинарни део комплексног броја $z$.

Алгебарски облик комплексног броја је

$z=x+iy$ za $x,y\in ℝ$

Тригонометријски облик комплексног броја је

$z=r(cos\theta +isin\theta ),r\ge 0,\theta \in ℝ$

pri čemu je

$r=\mid z\mid$ модул

$\theta =ARgz$ аргумент

Експоненцијални облик комплексног броја је

$z=r^{i\theta }$ za $r\ge 0,\theta \in ℝ$

при чему је

$r=\mid z\mid$ модул

$\theta =ARgz$ аргумент

Два комплексна броја су једнака ако су им једнаки реални и имагинарни делови.

$z_1=z_2\leftrightarrow (\mathrm{Re}(z_1)=\mathrm{Re}(z_2)\wedge \mathrm{Im}(z_1)=\mathrm{Im}(z_2)).$

Коњуговано комплексни број броја $z=x+iy$ је број $\overline{z}=x-iy$.

Модул или апсолутна вредност комплексног броја $z$ је ненегативни реални број $r=|z|=\sqrt{x^2+y^2}$.

Особине сабирања комплексних бројева

$(z_1+z_2=z_2+z_1$ za $\mathrm{\forall }{z}_1,z_2\in ℂ$ комутативност сабирања

$z_1+(z_2+z_3)=(z_1+z_2)+z_3,$ za $\mathrm{\forall }{z}_1,z_2,z_3\in ℂ$ асоцијативност сабирања

$\mathrm{\exists }0\in ℂz+0=z$ za $\mathrm{\forall }z\in ℂ$ неутрални елемент 0(nula) за сабирање

Комплексни број $0=(0,0)=0+0i$

$(\mathrm{\forall }z\in ℂ)(\mathrm{\exists }(-z)\in ℂz+(-z)=0$ постојање инверзног елемента.

Комплексни број $-z=(-x,-y)=-x-yi$

Особине множења комплексних бројева

$(z_1*z_2=z_2*z_1$ za $\mathrm{\forall }{z}_1,z_2\in ℂ$ комутативност множења

$z_1*(z_2+z_3)=(z_1+z_2)+z_3$ za $\mathrm{\forall }{z}_1,z_2,z_3\in ℂ$ асоцијативност множења

$\mathrm{\exists }1\in ℂz*1=z$ za $\mathrm{\forall }z\in ℂ$ неутрални елемент $1$ за множење

$\mathrm{\forall }z\in ℂ)(z\ne 0)(\mathrm{\exists }{z}^{\prime }\in ℂz*(-z)=1$ постојање реципрочног елемента

$z_1*(z_2+z_3)=z_1*z_2+z_1*z_3$ za $\mathrm{\forall }{z}_1,z_2,z_3\in ℂ$ дистрибутивност множења у односу на сабирање

Реалан производ два комплексна броја

У скупу комплексних бројева скаларном производу вектора одговара појам реалног производа комплексних бројева који је скаларни производ вектора који су одређени комплексним бројевима који се множе.

Дефиниција

Реалан производ комплексних бројева $a$ i $b$, у ознаци $a\circ b$, је реалан број одређен као

$a\circ b=\frac{1}{2}(\bar{a}b+a\bar{b})$

Нека су -{A}- и -{B}- тачке одређене комплексним бројевима $a=\mid a\mid (cos\phi +isin\phi )$ i$b=\mid b\mid (cos\psi +isin\psi )$ Лако је проверити да је

$a\circ b=\mid a\mid \mid b\mid (cos\phi +isin\psi )=\mid OA\mid \mid AB\mid cos\widehat{AOB}$

Особине реалног производа два комплексна броја

1. $a\circ a=\mid a{\mid }^2$
2. $a\circ b=b\circ a$
3. $\overline{a\circ b}=a\circ b$
4. $(\alpha a)\circ b=\alpha (a\circ b)=a\circ (\alpha b)$
5. $(az))bz)=\mid z{\mid }^2(a\circ b)$
6. $a\circ b=0<=>OA\perp OB$ (за тачке -{A}- и -{B}- комплексне равни одређене комплексним бројевима $a$ и $b$)

Реалан производ комплексних бројева $a$ и $b$ једнак је потенцији координатног почетка $O$ комплексне равни у односу на круг чији је пречник $AB$, где су $A$ и $B$ тачке комплексне равни одређене комплексним бројевима $a$ Q $b$.

Тачка $M$ је средина дужи -{AB}- одређена комплексним бројем $\frac{a+b}{2}$, потенција тачке $O$ у односу на круг са средиштем у тачки $M$ и полупречником

$r=\frac{a-b}{2}=\frac{\mid a-b\mid }{2}$ једнака је

$O{M}^2-r^2=\mid \frac{a+b}{2}\mid -\mid \frac{a-b}{2}\mid =\frac{(a+b)(\bar{a}+\bar{b}}{4}-\frac{(a-b)(\bar{a}-\bar{b})}{4}=a\circ b$

Нека су тачке $A$,$B$,$C$,$D$ тачке комплексне равни одређене комплексним бројевима $a$, $b$, $c$, $d$. Тада су следећа тврђења еквивалентна:

1. $AB\perp CD$
2. $(a+b)\circ (c+d)=0$
3. $\frac{b-a}{d-c}\in iℝ\left\{\begin{array}{c}0\end{array}\right\}$
4. $Re(\frac{b-a}{d-c})=0$

Средиште кружнице описане око троугла $ABC$ налази се у координатном почетку комплексне равни. Ако су темена $A$, $B$, $C$ троугла $ABC$ одређена комплексним бројевима $a$, $b$, $c$ респективно, тада је ортоцентар $H$ тог троугла одређен комплексним бројем $h=a+b+c$.

Комплексан производ два комплексна броја

Комплексан производ два комплексна броја је аналоган векторском производу вектора.

Дефиниција

Комплексан број

$a\times b=\frac{\bar{a}b-a\bar{b}}{2}$ називамо комплексним производом комплексних бројева $a$ и $b$.

Нека су $A$ и $B$ тачке одређене комплексним бројевима $a=\mid a\mid (cos\phi +isin\phi )$ и $a=\mid b\mid (cos\psi +isin\psi )$ Лако је провјерити да је

$\mid a\times b\mid =\mid a\mid \mid b\mid sin(\phi -\psi )=\mid OA\mid \mid AB\mid sin\widehat{AOB}=2P_{AOB}$

Нека су $a$, $b$, $c$ комплексни бројеви. Тада комплексан производ два комплексна броја има следеће особине

1. $\overline{a\times b}=-a\times b$
2. $a\times b=0<=>a=0\vee b=0\vee a=\lambda b$ gdje je $\lambda \in ℝ\left\{\begin{array}{c}0\end{array}\right\}$
3. $a\times b=-b\times a$
4. $\alpha (a\times b)=(\alpha a)\times b=a\times (\alpha b)$ ( $\mathrm{\forall }\alpha \in ℝ$ )

Ако су $A(a)$ и $B(b)$ две различите тачке различите од $O(0)$, тада је $a\times b=0$ onda i samo onda ako su $O$, $A$,$B$ колинеарне тачке.

Нека су $A(a$) и $B(b$) две различите тачке у комплексној равни различите од координатног почетка. Комплексан производ бројева $a$ и $b$ има следећи геометријски смисао

$a\times b=\{\begin{array}{c}2i{P}_{AOB}zatrougaoAOBpozitivnoorijentisan\\ -2i{P}_{AOB}zatrougaoAOBnegativnoorijentisan\end{array}$ Нека су $A(a)$, $B(b)$ и $C(c)$ три различите тачке у комплексној равни.

Тада је

$P_{ABC}=\{\begin{array}{c}\frac{1}{2}(a\times b+b\times c+c\times a)akojeABCpozitivnoorijentisan\\ \frac{1}{2}(a\times b+b\times c+c\times a)akojeABCnegativnoorijentisan\end{array}$

Нека су $A(a)$, $B(b)$ и $C(c)$ три различите тачке у комплексној равни.

Тада су следећа тврђења еквивалентна

1. Тачке $A$,$B$,$C$ су колинеарне
2. $(b-a)\times (c-a)=0$
3. $a\times b+b\times c+c\times a=0$

Нека су $A(a)$, $B(b)$, $C(c)$ и $D(d)$ четири тачке од којих ни једна група од три нису колинеарне. Тада је $AB\parallel CD$ онда и само онда ако је $(b-a)\times (d-c)=0$

Дељење комплексних бројева

$\frac{z_1}{z_2}=\frac{x_1+i{y}_1}{x_2+i{y}_2}\cdot \frac{x_2-i{y}_2}{x_2-i{y}_2}=\frac{x_1{x}_2+y_1{y}_2}{x_2^2+y_2^2}+i\frac{y_1{x}_2-x_1{y}_2}{x_2^2+y_2^2},\text{za}{z}_2\ne 0$

У сваком скупу бројева дељење се дефинише као множење инверзним елементом. Уверимо се да за

$\mathrm{\forall }z\in ℂ)(z\ne 0)\mathrm{\exists }{z}^{\prime }\in ℂ$

Нека је $z=x+yi\ne 0$ bilo koji. Onda je $x^2+y^2\ne 0$ па је добро дефинисан број

$z^{\prime }=\frac{x}{x^2+y^2}+\frac{-y}{x^2+y^2}i$

$\frac{1}{z}=\frac{\overline{z}}{z\overline{z}}=\frac{\overline{z}}{x^2+y^2}=\frac{x}{x^2+y^2}-\frac{y}{x^2+y^2}i.$

имамо

$z^{\prime }*z=z*z^{\prime }=1$

$z^{\prime }=z^{-1}=\frac{1}{z}$

Коњуговано комплексни бројеви

Коњуговано комплексни бројеви

Комплексан број $\bar{z}=x-yi=r^{-i\theta }$ називамо коњугованим бројем $z=x+yi=r^{i\theta }$.

Бројеви $z$ i $\bar{z}$ чине пар коњугованих бројева. Њиховим сабирањем и одузимањем добијамо

$Rez=\frac{1}{2}(z+\bar{z})$

$Imz=\frac{1}{2i}(z-\bar{z})$

Лако се проверава да вреди

1. $\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}$
2. $\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}$
3. $\overline{z_1*z_2}=\overline{z_1}*\overline{z_2}$
4. $\overline{(\frac{z_1}{z_2})}=\frac{\overline{z_1}}{\overline{z_1}}$

Neka je $z=r(cos\theta +isin\theta )=rcis\theta$ тригонометријски облик комплексног броја. Тада је

$z^2=z*z$

$z^2=rcis\theta *rcis\theta =r^{2}cis(\theta +\theta )=r^{2}cis2\theta$

$z^3=r^{2}cis2\theta *rcis\theta =r^{3}cis(2\theta +\theta )=r^{3}cis3\theta$

$z^4=r^{3}cis3\theta *rcis\theta =r^{4}cis(3\theta +\theta )=r^{4}cis4\theta$

На овај начин добијамо општи облик Де Моавровог теорема који има важну улогу у електротехници

$z^n=r^{n}cisn\theta$ Q

$(cos\theta +isin\theta {)}^n=cosn\theta +isinn\theta (n\in Z)$

Степеновање комплексног броја

$z^n=r^n(cosn\theta +isinn\theta )=r^n{e}^{in\theta }$ za $n\in N$.

$z^m{z}^n=z^{m+n}$

$(z_1{z}_2{)}^n=(z_1{z}_2{)}^n$

$(z^m{)}^n=z^{mn}$

Кореновање комплексног броја

$\sqrt[n]{z}=\left\{\begin{array}{c}{u}_0,u_1...u_n\end{array}\right\}$ за $n\in N$

где је

$u_k=\sqrt[n]{r}(cos\frac{\sqrt[n]{r}}{n}+isin\frac{\theta +2k\pi }{n})$ za $k=0,1...(n-1)$

$u_k=\sqrt[n]{r}{e}^{i(\theta +2k\pi )/2}$ za $k=0,1...(n-1)$

Квадратни корен имагинарног броја

$\sqrt{i}=\frac{1}{2}\sqrt{2}+i\frac{1}{2}\sqrt{2}=\frac{\sqrt{2}}{2}(1+i).$

Овај резултат можемо добити на следећи начин

$i=(a+bi{)}^2$

$i=a^2+2abi-b^2.$

Добијамо две једначине

$\{\begin{array}{c}2ab=1\\ a^2-b^2=0\end{array}$

чија су решења

$a=b=\pm \frac{1}{\sqrt{2}}.$

Избор главног корена даје

$a=b=\frac{1}{\sqrt{2}}.$

Резултат можемо добити помоћу Моаврове формуле

$i=\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right)$

$\begin{array}{cc}\sqrt{i}& ={(\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right))}^{\frac{1}{2}}\\ & =\cos \left(\frac{\pi }{4}\right)+i\sin \left(\frac{\pi }{4}\right)\\ & =\frac{1}{\sqrt{2}}+i\left(\frac{1}{\sqrt{2}}\right)=\frac{1}{\sqrt{2}}(1+i).\\ \end{array}$

Апсолутна вредност аргумента

Апсолутна вредност (или модул или величине) комплексног броја $z=x+yi$ je

$r=|z|=\sqrt{x^2+y^2}.$

Квадрат апсолутне вредности је

$|z{|}^2=z\overline{z}=x^2+y^2.$

$\phi =\arg (z)=\{\begin{array}{cc}\arctan (\frac{y}{x})& \text{if }x>0\\ \arctan (\frac{y}{x})+\pi & \text{if }x<0\text{ and }y\ge 0\\ \arctan (\frac{y}{x})-\pi & \text{if }x<0\text{ and }y<0\\ \frac{\pi }{2}& \text{if }x=0\text{ and }y>0\\ -\frac{\pi }{2}& \text{if }x=0\text{ and }y<0\\ \text{indeterminate }& \text{if }x=0\text{ and }y=0.\end{array}$

Множење и дељење у поларном облику

Из тригонометријских идентитета

$\cos (a)\cos (b)-\sin (a)\sin (b)=\cos (a+b)$

$\cos (a)\sin (b)+\sin (a)\cos (b)=\sin (a+b)$

имамо

$z_1{z}_2=r_1{r}_2(\cos ({\phi }_1+{\phi }_2)+i\sin ({\phi }_1+{\phi }_2)).$

Пример

$(2+i)(3+i)=5+5i.$

$\frac{\pi }{4}=\arctan \frac{1}{2}+\arctan \frac{1}{3}$

Дељење

$\frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos ({\phi }_1-{\phi }_2)+i\sin ({\phi }_1-{\phi }_2)).$

Тригонометријски облик

Понекад је комплексне бројеве погодно писати у тригонометријском облику:

$a+bi=\rho (\cos \varphi +i\sin \varphi )$,

$\rho =\sqrt{a^2+b^2},\varphi =\arctan \frac{b}{a}$, за $a>0$ и $\varphi =\pi +\arctan \frac{b}{a}$ за $a<0$; када је $a=0$ онда је $\varphi =\frac{\pi }{2}$, ако је $b>0$ и $\varphi =-\frac{\pi }{2}$, ako je $b<0$. Број $\rho$ се назива модуо комплексног броја, а $\varphi$ је аргумент комплексног броја.

Множити комплексне бројеве је веома погодно баш у овом облику.

У множењу комплексних бројева множе се њихови модули, а аргументи се сабирају. $r_1(\cos {\varphi }_1+i\sin {\varphi }_1)\cdot r_2(\cos {\varphi }_2+i\sin {\varphi }_2)=r_1{r}_2(\cos ({\varphi }_1+{\varphi }_2)+i\sin ({\varphi }_1+{\varphi }_2))$.

слично је и за дељење. $\frac{r_1(\cos {\varphi }_1+i\sin {\varphi }_1)}{r_2(\cos {\varphi }_2+i\sin {\varphi }_2)}=\frac{r_1}{r_2}(\cos ({\varphi }_1-{\varphi }_2)+i\sin ({\varphi }_1-{\varphi }_2))$.

Из овог правила произлази Моаврова формула:

$(\cos \varphi +i\sin \varphi {)}^n=\cos n\varphi +i\sin n\varphi$ .

Комплексни бројеви се често представљају векторима у комплексној равни (слика доле). Геометријски смисао бројева $a,b,\rho ,\varphi$ види се на цртежу. У сабирању комплексних бројева њихови вектори се сабирају по правилу паралелограма.

Комплексна раван

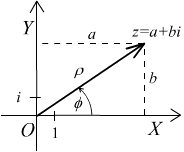
Дужина вектора $\rho$ је модуо, или модул комплексног броја, а као што се види на горњој слици, може се добити помоћу Питагорине теореме. Модул, интензитет комплексног броја често означавамо као апсолутну вредност, тј. удаљеност броја од исходишта координатног система: $|z|=\rho =\sqrt{a^2+b^2}$.

Комплексни бројеви у тригонометријском облику су уско повезани с експоненцијалном функцијом имагинарног аргумента. Важи следећа Ојлерова формула:

$e^{i\varphi }=\cos \varphi +i\sin \varphi$;

помоћу ње се дефинише степеновање комплексних бројева, логаритам комплексног броја и др.

Комплексни бројеви образују алгебарско затворено поље. Поље комплексних бројева је проширење поља реалних бројева придруживањем овом пољу елемента $i$, таквог да је $i^2=-1$.

Множење

Множење комплексних бројева у тригонометријском облику је слично множењу комплексних бројева у стандардном облику.

Нека су задани комплексни бројеви

$z_1=r_1(cos{\phi }_1+isin{\phi }_1)$ i $z_2=r_2(cos{\phi }_2+isin{\phi }_2)$

онда је

$z_1{z}_2=r_1(cos{\phi }_1+isin{\phi }_1)r_2(cos{\phi }_2+isin{\phi }_2)=$

$r_1{r}_2(cos{\phi }_{1}cos{\phi }_2+icos{\phi }_{1}sin{\phi }_2+icos{\phi }_{2}sin{\phi }_1+i^{2}sin{\phi }_{1}sin{\phi }_2)=$

$r_1{r}_2((cos{\phi }_{1}cos{\phi }_2-sin{\phi }_{1}sin{\phi }_2)+i(cos{\phi }_{1}sin{\phi }_{2}cos{\phi }_{2}sin{\phi }_1))=$

$r_1{r}_2(cos({\phi }_1+{\phi }_2)+isin({\phi }_1+{\phi }_2))$

Дељење

Нека су задати комплексни бројеви

$z_1=r_1(cos{\phi }_1+isin{\phi }_1)$ i $z_2=r_2(cos{\phi }_2+isin{\phi }_2)$

$\frac{z_1}{z_2}=\frac{r_1(cos{\phi }_1+isin{\phi }_1)}{r_2(cos{\phi }_2+isin{\phi }_2)}=\frac{r_1(cos{\phi }_1+isin{\phi }_1)}{r_2(cos{\phi }_2+isin{\phi }_2)}*\frac{(cos{\phi }_2-isin{\phi }_2)}{(cos{\phi }_2-isin{\phi }_2)}$

$\frac{r_1}{r_2}*\frac{cos{\phi }_{1}cos{\phi }_2-icos{\phi }_{1}sin{\phi }_2+icos{\phi }_{2}sin{\phi }_1-i^{2}sin{\phi }_{1}sin{\phi }_2}{co{s}^2{\phi }_2+si{n}^2{\phi }_2}$

$\frac{r_1}{r_2}(cos({\phi }_1-{\phi }_2)+isin({\phi }_1-{\phi }_2))=\frac{r_1}{r_2}(cis({\phi }_1-{\phi }_2)$

Де Моаврова формула

Нека је

$z=r(cos\theta +isin\theta )=rcis\theta$ тригонометријски облик комплексног броја. Тада је

$z^2=z*z$

$z^2=rcis\theta *rcis\theta =r^{2}cis(\theta +\theta )=r^{2}cis2\theta$

$z^3=r^{2}cis2\theta *rcis\theta =r^{3}cis(2\theta +\theta )=r^{3}cis3\theta$

$z^4=r^{3}cis3\theta *rcis\theta =r^{4}cis(3\theta +\theta )=r^{4}cis4\theta$

На овај начин добијамо општи облик Де Моаврове теореме који има важну улогу у електротехници

$(\cos \varphi +i\sin \varphi {)}^n=\cos n\varphi +i\sin n\varphi$

Поларни облик

Аргумент Шаблон:Mvar и модуо Шаблон:Mvar лоцирају тачку на Аргандовом дијаграму; $r(\cos \phi +i\sin \phi )$ или $r{e}^{i\phi }$ су поларни изрази за тачку.

Апсолутна вредност и аргумент

Један алтернативни начин дефинисања тачке -{P}- у комплексној равни, осим коришћења x- и y- координата, је употреба растојања тачака од O, тачке чије су координате Шаблон:Math (координатни почетак), заједно са углом између позитивне реалне осе и линијског сегмента -{OP}- у смеру наупрот кретања казаљки на сату. Ова идеја производи поларни облик комплексних бројева.

Апсолутна вредност (или модуо или магнитуда) комплексног броја Шаблон:Math је

$r=|z|=\sqrt{x^2+y^2}.$

Ако је Шаблон:Mvar реални број (нпр., Шаблон:Math), онда је Шаблон:Math. Генерално, по Питагориној теореми, Шаблон:Mvar је растојање од тачке -{P}- која представља комплексни број Шаблон:Mvar до координатног почетка. Квадрат апсолутне вредности је

$|z{|}^2=z\overline{z}=x^2+y^2.$

где је $\overline{z}$ комплексно конјуговани број од $z$.

Аргумент Шаблон:Mvar (који се у многим применама назива „фазом“) је угао полупречника -{OP}- са позитивном реалном осом, и пише се као $\arg (z)$. Као и код модула, аргумент се може одредити из правоугаоног облика $x+yi$:

$\phi =\arg (z)=\{\begin{array}{cc}\arctan (\frac{y}{x})& \text{if }x>0\\ \arctan (\frac{y}{x})+\pi & \text{if }x<0\text{ and }y\ge 0\\ \arctan (\frac{y}{x})-\pi & \text{if }x<0\text{ and }y<0\\ \frac{\pi }{2}& \text{if }x=0\text{ and }y>0\\ -\frac{\pi }{2}& \text{if }x=0\text{ and }y<0\\ \text{indeterminate }& \text{if }x=0\text{ and }y=0.\end{array}$

Шаблон:Sndако је -{z}- реално, -{φ}- = 0 или Шаблон:Pi. Главни корени су приказани црном бојом.

Нормално, као што је дато горе, главна вредност се разматра на интервалу Шаблон:Open-closed. Вредности у опсегу Шаблон:Closed-open се добијају додавањем Шаблон:Math ако је вредност негативна. Вредност Шаблон:Mvar се изражава у радијанима угла. Она може да буде повећана за целобројни умножак од Шаблон:Math и да се још увек односи на исти угао. Стога се -{arg}- функција понекад сматра мултивредносном. Поларни угао комплексног броја 0 је неодређен, мада се арбитрарни избор угла 0 често прави.

Вредност Шаблон:Mvar је једнака резултату atan2:

$\phi =\text{atan2}(\mathrm{Im}(z),\mathrm{Re}(z)).$

Заједно, Шаблон:Mvar и Шаблон:Mvar дају један додатни начин приказивања комплексних бројева, поларни облик, пошто комбинација модула и аргумента у потпуности специфицирају позицију тачке у равни. Оригиналне правоугаоне координате се могу извести из поларних применом формула званих тригонометријска форма

$z=r(\cos \phi +i\sin \phi ).$

Користећи Ојлерову формулу ово се може записати као

$z=r{e}^{i\phi }.$

Користећи -{cis}- функцију, тај израз се понекад скраћује на

$z=r\mathrm{cis}\phi .$

У угаоној нотацији, који асе често користи у електроници за приказивање вектора са амплитудом Шаблон:Mvar и фазом Шаблон:Mvar, то се може записати као

$z=r\mathrm{\angle }\phi .$

Множење и дељење у поларном облику

[[Датотека:Complex multi.svg|десно|мини|Множење Шаблон:Math (плави троугао) и Шаблон:Math (црвени троугао). Црвени троугао се ротира да се поклопи са највишом тачком плавог и прошири се за [[квадратни корен од 5|Шаблон:Sqrt]], дужину хипотенузе плавог троугла.]]

Формуле за множење, дељење и степеновање су једноставније у поларном облику него кореспондирајуће формуле у Картезијанским координатама. За два дата комплексна броја Шаблон:Math и Шаблон:Math, због добро познатих тригонометријских релација

$\cos (a)\cos (b)-\sin (a)\sin (b)=\cos (a+b)$

$\cos (a)\sin (b)+\sin (a)\cos (b)=\sin (a+b)$

се може извести

$z_1{z}_2=r_1{r}_2(\cos ({\phi }_1+{\phi }_2)+i\sin ({\phi }_1+{\phi }_2)).$

Другим речима, апсолутне вредности се множе а аргументи се додају чиме се добија поларни облик производа. На пример, множење са Шаблон:Math је истоветно са заокретом за четвртину круга у смеру супротном кретању казаљки на сату, чиме се производи Шаблон:Math. Слика на десној страни илуструје множење

$(2+i)(3+i)=5+5i.$

Пошто су реални и имагинарни део броја Шаблон:Math једнаки, аргумент тог броја је 45 степени, или π/4 (у радијанима). С друге стране, то је исто тако сума углова у координатном почетку црвеног и плавог троугла, који су -{arctan}-(1/3) и -{arctan}-(1/2). Стога формула

$\frac{\pi }{4}=\arctan \frac{1}{2}+\arctan \frac{1}{3}$

важи. Пошто се -{arctan}- функција може веома ефикасно апроксимирати, формуле попут ове —познате као формуле сличне Машиновим — се користе за апроксимације високе прецизности вредности π.

Слично томе, дељење је дато изразима

$\frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos ({\phi }_1-{\phi }_2)+i\sin ({\phi }_1-{\phi }_2)).$

Матрични облик

$(a+ib):=\left[\begin{array}{cc}a& -b\\ b& a\end{array}\right]$

У матричном облику сабирање, одузимање и множење радимо тако што сабирамо, одузимамо и множимо одговарајуће матрице које представљају комплексан број.

Реципрочну вредност у овом запису рачунамо тражењем инверзне матрице. Дељење дефинишемо као множење реципрочном вредношћу.

Литература

• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Springer
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book. by Roger Penrose; Alfred A. Knopf. Chapters 4–7 in particular deal extensively (and enthusiastically) with complex numbers.
• -{Шаблон:Cite book. by John Derbyshire; Joseph Henry Press. (hardcover 2006). A very readable history with emphasis on solving polynomial equations and the structures of modern algebra.}-
• -{Шаблон:Cite book. by Tristan Needham; Clarendon Press. (hardcover, 1997). History of complex numbers and complex analysis with compelling and useful visual interpretations.}-
• Шаблон:Cite book-

Спољашње везе

• Шаблон:Springer
• -{Introduction to Complex Numbers from Khan Academy}-
• Шаблон:In Our Time
• -{Euler's Investigations on the Roots of Equations at Convergence. MAA Mathematical Sciences Digital Library.}-
• -{John and Betty's Journey Through Complex Numbers}-
• -{The Origin of Complex Numbers by John H. Mathews and Russell W. Howell}-
• -{Dimensions: a math film. Chapter 5 presents an introduction to complex arithmetic and stereographic projection. Chapter 6 discusses transformations of the complex plane, Julia sets, and the Mandelbrot set.}-