Bezjeove krive

Bezjeove krive su parametarske krive. Njihovu najbolju primenu pronalazimo u računarskoj grafici.

Zadaju se određenim brojem kontrolnih tačaka čijim se pomeranjem menja oblik krive. Dodavanjem kontrolnih tačaka se povećava stepen krive, ali i složenost izračunavanja, zbog čega se najčešće koriste krive malog stepena. Takozvanim „lepljenjem“ krivih malog stepena, dobijaju se Bezjeovi splajnovi (složene krive).

Pol Kastelžo i Pjer Bezje su ih prvi koristili pri dizajnu automobila krajem pedesetih godina dvadesetog veka.

Definicija Bezjeove krive

Rekurzivna definicija

Ako Bezjeovu krivu određenu pomoću tački $P_0,P_1,...P_n$ označimo kao ${\alpha }_{P_0{P}_1...P_n}$. Onda:

${\mathit{\alpha }}_{{𝐏}_0}(t)={𝐏}_0$ i

$\mathit{\alpha }(t)={\mathit{\alpha }}_{{𝐏}_0{𝐏}_1\dots {𝐏}_n}(t)=(1-t){\mathit{\alpha }}_{{𝐏}_0{𝐏}_1\dots {𝐏}_{n-1}}(t)+t{\mathit{\alpha }}_{{𝐏}_1{𝐏}_2\dots {𝐏}_n}(t)$

Eksplicitna definicija

Neka je Bezjeova kriva, stepena $n\ge 2$, zadata pomoću $P_0,P_1,P_2..P_n,n\ge 2$ tačaka ravni. Možemo je predstaviti sledećim polinomom:

${\alpha }_n(t)=\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})t^i(1-t{)}^{n-i}{P}_i=\sum _{i=0}^n{B}_i^n(t)P_i,t\in [0,1].$

Tačke $P_i$ pomoću kojih je definisana kriva nazivaju se kontrolne tačke, a polinomi $B_i^n$ Bernstajnovi polinomi, tj. bazne funkcije.

Tačke $P_0,P_1,P_2..P_n$ obrazuju kontrolni poligon.

Polinomijalni oblik

Primenom binomne teoreme na definiciju krive dobijamo:

$\mathit{\alpha }(t)=\sum _{j=0}^n{t}^j{𝐂}_j$

gde je:

${𝐂}_j=\frac{n!}{(n-j)!}\sum _{i=0}^j\frac{(-1{)}^{i+j}{𝐏}_i}{i!(j-i)!}=\prod _{m=0}^{j-1}(n-m)\sum _{i=0}^j\frac{(-1{)}^{i+j}{𝐏}_i}{i!(j-i)!}.$

Izvod

Izvod krive stepena $n$ je:

${\mathit{\alpha }}^{\prime }(t)=n\sum _{i=0}^{n-1}{b}_{i,n-1}(t)({𝐏}_{i+1}-{𝐏}_i)$

Specijalni slučajevi

Najveću praktičnu primenu imaju Bezjeove krive drugog i trećeg stepena.

Linearna Bezjeova kriva

Bezjeova kriva stepena 1, tj. kriva određena sa samo dve tačke $P_0$ i $P_1$, jeste zapravo duž $P_0{P}_1$, zadata sledećom parametrizacijom:

${\alpha }_1(t)=(1-t)P_0+t{P}_1,t\in [0,1].$

Kvadratna Bezjeova kriva

Bezijerova kriva drugog stepena

Bezjeova kriva drugog stepena je deo parabole

Kvadratna Bezjeova kriva zadata je sledećom parametrizacijom:

${\alpha }_2(t)=(1-t{)}^2{P}_0+2t(1-t)P_1+t^2{P}_2,t\in [0,1].$

Bezjeova kriva drugog stepena je deo parabole. Dokaz leži u osobini invarijantnosti afinih preslikavanja.

Izvod:

${\mathit{\alpha }}^{″}(t)=2({𝐏}_2-2{𝐏}_1+{𝐏}_0).$

Kubna Bezjeova kriva

Bezjeova kriva trećeg stepena

Kriva je zadata pomoću tačaka $P_0,P_1,P_2,P_3$ . Počinje u $P_0$, ide prema $P_1$ i stiže u $P_3$ dolazeći iz smera $P_2$. Uglavnom ne prolazi kroz $P_1$ i $P_2$; ove tačke služe da obezbede dodatne informacije (razdaljina između $P_0$ i $P_1$ određuje „koliko daleko“ i „koliko brzo“ se kriva kreće prema $P_1$ pre nego što skrene ka $P_2$).

Kubna Bezjeovakriva zadata je sledećom paramtrizacijom:

${\alpha }_3(t)=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3,t\in [0,1].$

Prvi izvod:

${\mathit{\alpha }}^{\prime }(t)=3(1-t{)}^2({𝐏}_1-{𝐏}_0)+6(1-t)t({𝐏}_2-{𝐏}_1)+3t^2({𝐏}_3-{𝐏}_2).$

Drugi izvod:

${\mathit{\alpha }}^{″}(t)=6(1-t)({𝐏}_2-2{𝐏}_1+{𝐏}_0)+6t({𝐏}_3-2{𝐏}_2+{𝐏}_1).$

Osobine Bezjeovih krivih

• Najveći stepen Bezjeove krive ${\alpha }_n$ definisane sa $n+1$ kontrolnih tačaka je $n$.
• Početna tačka krive je $P_0$, tj. ${\alpha }_n(0)=P_0$
• Vektor $\overrightarrow{P_0{P}_1}$ je kolinearan tangentnom vektoru krive u tački $P_0$ dok je vektor $\overrightarrow{P_{n-1}{P}_n}$ kolinearan tangentnom vektoru krive $P_n$.
• Osobina nenegativnosti: za $t\in [0,1]$ možemo videti da su svi Bernstajnovi polinomi $B_i^n\in [0,1]$, tj. nenegativni su.
• Osobina konveksnog omotača: Bezjeova kriva koja je određena pomoću $n+1$ kontrolnih tačka pripada konveksnom omotaču tih tačka. Centar mase tačaka $P_0(B_0^n(t)),...,P_n(B_n^n(t))$ sa pridruženim pozitivnim masama je tačka ${\alpha }_n(t)$. Na slici je prikazana kriva 6. stepena, a konveksni omotač njenih 7 kontrolnih tačaka je označen roze bojom. Izuzev dve krajnje tačke koje su na rubu, čitava kriva leži unutar omotača.

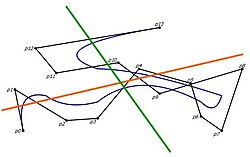Konveksni omotač Bezjeove krive		Osobina manje varijacije

• Osobina manje varijacije: nijedna prava ne preseca Bezijerovu krivu više puta nego što seče kontrolnu poligonsku liniju.
• Osobina afine invarijantnosti: slika Bezjeove krive pri afinom preslikavanju je određena slikama njenih kontrolnih tačaka pri tom istom preslikavanju.

Bezjeova kriva na proizvoljnom segmentu

Osnovni domen Bezjeove krive je segment $[0,1]$, ali ga možemo proširiti na proizvoljni segment. U tom slučaju je potrebno izvršiti smenu promenljive $t$ na sledeći način:

$u=\frac{t-a}{b-a}$

Sada je promenljiva $u$ definisana na intervalu $[0,1]$ i potrebno ju je zameniti u bazne funkcije kako bi kriva bila definisana na segmentu $[a,b]$:

$B_{n,i}(t)=\frac{n!}{i!(n-i)!}{\left(\frac{t-a}{b-a}\right)}^i{(1-\frac{t-a}{b-a})}^{n-i}$

Pomeranje kontrolnih tačaka

Pomeranje kontrolne tačke Bezjeove krive

Pretpostavimo da je kontrolna tačka $P_k$ pomerena za vektor $\overrightarrow{v}$.

Nova kriva je određena tačkama $P_0,P_1,\cdots ,P_k+\overrightarrow{v},\cdots ,P_n$ i njena jednačina je:

$\begin{array}{cc}\beta (t)& =\sum _{i=0}^{k-1}{B}_{n,i}(t)P_i+B_{n,k}(t)(P_k+\overrightarrow{v})+\sum _{i=k+1}^n{B}_{n,i}(t)P_i\\ & =\sum _{i=0}^n{B}_{n,i}(t)P_i+B_{n,k}(t)\overrightarrow{v}\\ & =\alpha (t)+B_{n,k}(t)\overrightarrow{v}\end{array}$

Nova kriva se predstavlja kao zbir početne krive i dodatnog člana $B_{n,k}(t)\overrightarrow{v}.$ Tačka $\alpha (t)$ na novoj krivoj je dobijena translacijom tačke $\alpha (t)$ na početnoj krivoj u pravcu $\overrightarrow{v}$ na rastojanju $\left|\begin{array}{c}{B}_{n,k}(t)\overrightarrow{v}\end{array}\right|$. Osim krajnjih tačaka, sve tačke početne krive se pomeraju na nove pozicije.

Pomeranje bilo koje kontrolne tačke Bezjeove krive menja krivu globalno.

Početna kriva na slici je kriva 8. stepena sa 9 kontrolnih tačaka i označena je crnom bojom. Ako kontrolnu tačku $P_3$ pomerimo na novu poziciju, crna kriva se menja u crvenu.

Matrična reprezentacija

Kvadratne Bezjeove krive

$(1,t,t^2)\left[\begin{array}{ccc}1& 0& 0\\ -2& 2& 0\\ 1& -2& 1\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\end{array}\right]$

Kubne Bezjeove krive

$\left[\begin{array}{cccc}1& t& t^2& t^3\end{array}\right]M$$\left[\begin{array}{c}{P}_o\\ P_1\\ P_2\\ P_3\end{array}\right]$

Gde je $M=\left[\begin{array}{cccc}1& 0& 0& 0\\ -3& 3& 0& 0\\ 3& -6& 3& 0\\ -1& 3& -3& 1\end{array}\right]$

Odakle se analogijom dobija uopštenje:

$\left[\begin{array}{cccccc}1& t& t^2& t^3& \cdots & t^n\end{array}\right]M$$\left[\begin{array}{c}{P}_o\\ P_1\\ P_2\\ P_3\\ ⋮\\ P_n\end{array}\right]$

Podela Bezjeove krive na dva dela korišćenjem matrične reprezentacije

Kvadratna Bezjeova kriva

Razmotrimo sad podelu krive na dva dela pravljenjem reza u tački $\alpha (t)=\alpha (t_0),t,t_0\in [0,1]$.

Prva kriva:

$\begin{array}{cc}{\beta }_2^1(t)& =(1,t,t^2)M{S}_{[0,t_0]}(P_0,P_1,P_2{)}^T\end{array}$,

gde je $S_{[0,t_0]}$ data sa:

$\begin{array}{cc}{S}_{[0,t_0]}& =\left[\begin{array}{ccc}1& 0& 0\\ 1-t_0& t_0& 0\\ (1-t_0{)}^2& 2t_0(1-t_0)& t_0^2\end{array}\right].\end{array}$

Temena kontrolnog poligona dobijamo iz:

$S_{[0,t_0]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 1-t_0& t_0& 0\\ (1-t_0{)}^2& 2t_0(1-t_0)& t_0^2\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\end{array}\right]$

Za $t_0=\frac{1}{2}$ temena su data sa:

$S_{[0,\frac{1}{2}]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]$ $=\left[\begin{array}{c}{P}_0\\ \frac{1}{2}(P_0+P_1)\\ \frac{1}{4}(P_0+2P_1+P_2)\end{array}\right]$

Druga kriva ${\beta }_2^2(t)$ je definisana sa:

${\beta }_2^2(t)=\alpha (t_0+(1-t_0)t)=(1,t,t^2)M{S}_{[1-t_0,1]}(P_0,P_1,P_2{)}^T$,

gde je:

$S_{[1-t_0,1]}=\left[\begin{array}{ccc}(1-t_0{)}^2& -2t_0(1-t_0)& t_0^2\\ 0& (1-t_0)& t_0\\ 0& 0& 1\end{array}\right]$.

Kontrolni poligon je određen sledećim tačkama:

$S_{[1-t_0,1]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\end{array}\right]=\left[\begin{array}{ccc}(1-t_0{)}^2& -2t_0(1-t_0)& t_0^2\\ 0& (1-t_0)& t_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\end{array}\right]$.

tj. za $t_0=\frac{1}{2}$:

$S_{[\frac{1}{2},1]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\end{array}\right]$ $=\left[\begin{array}{c}\frac{1}{4}(P_0+2P_1+P_2)\\ \frac{1}{2}(P_1+P_2)\\ P_2\end{array}\right]$

Kubna Bezjeova kriva

Razmotrimo sad podelu krive na dva dela pravljenjem reza u tački $\alpha (t)=\alpha (t_0),t,t_0\in [0,1]$.

Prva kriva:

$\begin{array}{cc}{\beta }_3^1(t)& =(1,t,t^2,t^3)M{S}_{[0,t_0]}(P_0,P_1,P_2,P_3{)}^T\end{array}$,

gde je $S_{[0,t_0]}$ data sa:

$\begin{array}{cc}{S}_{[0,t_0]}& =\left[\begin{array}{cccc}1& 0& 0& 0\\ 1-t_0& t_0& 0& 0\\ (1-t_0{)}^2& 2t_0(1-t_0)& t_0^2& 0\\ (1-t_0{)}^2& 3t_0(1-t_0{)}^2& 3t_0^2(1-t_0)& t_0^3\end{array}\right].\end{array}$

Temena kontrolnog poligona dobijamo iz:

$S_{[0,t_0]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 1-t_0& t_0& 0& 0\\ (1-t_0{)}^2& 2t_0(1-t_0)& t_0^2& 0\\ (1-t_0{)}^2& 3t_0(1-t_0{)}^2& 3t_0^2(1-t_0)& t_0^3\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]$

Za $t_0=\frac{1}{2}$ temena su data sa:

$S_{[0,\frac{1}{2}]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]$ $=\left[\begin{array}{c}{P}_0\\ \frac{1}{2}(P_0+P_1)\\ \frac{1}{4}(P_0+2P_1+P_2)\\ \frac{1}{8}(P_0+3P_1+3P_2+P_3)\end{array}\right]$

Druga kriva ${\beta }_3^2(t)$ je definisana sa:

${\beta }_3^2(t)=\alpha (t_0+(1-t_0)t)=(1,t,t^2,t^3)M{S}_{[1-t_0,1]}(P_0,P_1,P_2,P_3{)}^T$,

gde je:

$S_{[1-t_0,1]}=\left[\begin{array}{cccc}(1-t_0{)}^3& -3t_0(1-t_0{)}^2& 3t_0^2(1-t_0)& t_0^3\\ 0& (1-t_0{)}^2& 2t_0(1-t_0)& t_0^2\\ 0& 0& (1-t_0)& t_0\\ 0& 0& 0& 1\end{array}\right]$.

Kontrolni poligon je određen sledećim tačkama:

$S_{[1-t_0,1]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]=\left[\begin{array}{cccc}(1-t_0{)}^3& -3t_0(1-t_0{)}^2& 3t_0^2(1-t_0)& t_0^3\\ 0& (1-t_0{)}^2& 2t_0(1-t_0)& t_0^2\\ 0& 0& (1-t_0)& t_0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]$

tj. za $t_0=\frac{1}{2}$:

$S_{[\frac{1}{2},1]}\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]$ $=\left[\begin{array}{c}\frac{1}{8}(P_0+3P_1+3P_2+P_3)\\ \frac{1}{4}(P_1+2P_2+P_3)\\ \frac{1}{2}(P_2+P_3)\\ P_3\end{array}\right]$

De Kastelžoov algoritam

Ako želimo da odredimo tačku $\alpha (t),t\in [0,1]$ na krivoj, možemo jednostavno zameniti parametar u jednačinu krive. Ova metoda je numerički nestabilna i zato se koristi jednostavnija metoda: De Kastelžoov algoritam, čija je osnovna ideja u iterativnoj podeli kontrolnih duži u odnosu $t:(1-t)$.

Podela Bezjeove krive

Smisao podele krive je da je „isečemo“ u nekoj tački, tako da ona ostane podeljena na dva dela od kojih je svaki i dalje Bezjeova kriva. Početni skup kontrolnih tačaka se odbacuje, a rezultujuće Bezjeove krive se zadaju pomoću svojih novih kontrolnih tačkama.

Algoritam podele bazira se na De Kastelžoovom algoritmu.

Podela krive ima veliki broj primena: dizajn krivih, renderovanje Bezjeove krive, određivanje preseka dve krive... Ako imamo neku krivu koja nam ne odgovara, možemo je podeliti na nezadovoljavajući i zadovoljavajući deo i onda se skoncentrisati na promenu nezadovoljavajućeg dela.

Kriva se može deliti proizvoljan broj puta, a ako želimo da se podeoni preseci krive glatko spajaju, onda granične tačke i njihove dve susedne tačke moraju biti kolinearne.

Isto to važi ako želimo spojiti dve krive u jednu. Kako je crtanje krivih većeg stepena zahtevno, mogu se iskoristiti krive manjeg stepena i onda ih glatko povezivati.

Računarstvo

Kodiranje

Neki programski jezici omogućavaju crtanje Bezjeovih krivih ako su poznate kontrolne tačke kojima su određene.

Na primer, u -{html}--u napravimo -{canvas tag}-:

 <canvas id="myCanvas" width="500" height="300"></canvas>

U okviru -{JavaScript}--a definišemo -{canvas}- preko promenljivih:

 var c=document.getElementById("myCanvas");
 var ctx=c.getContext("2d");

Sada možemo koristiti sledeći kod koji iscrtava krivu stepena 3, gde $P_{i}x$ i $P_{i}y$ označavaju $x$ i $y$ koordinate $i$-te tačke.

 ctx.beginPath();
 ctx.moveTo(<math>P_0x,P_0y</math>);
 ctx.bezierCurveTo(<math>P_1x,P_1y,P_2x,P_2y,P_3x,P_3y</math>);
 ctx.stroke();

Ako želimo krivu drugog stepena, potrebno je pozvati odgovarajuću funkciju, tj.:

 ctx.beginPath();
 ctx.moveTo(<math>P_0x,P_0y</math>);
 ctx.quadraticCurveTo(<math>P_1x,P_1y,P_2x,P_2y</math>);
 ctx.stroke();

Naredni kod je jednostavan i praktičan primer koji prikazuje kako se crta kubna Bezjeova kriva u programskom jeziku -{C}-. Ovaj algoritam je linearan jer je u praksi brži i lakši za implementaciju, za razliku od rekurzivnog De Kastelžoovog algoritma koji se često pominje u računarskoj grafici.

/******************************************************
  Kod za generisanje kubne Bezjeove krive
 *******************************************************/
 
  typedef struct
  {
 	float x;
 	float y;
  }
  Point2D;
 
 /******************************************************
  cp je niz koji sadrži 4 elementa gde:
  cp[0] je početna tačka
  cp[1] je prva kontrolna tačka
  cp[2] je druga kontrolna tačka
  cp[3] je krajnja tačka
 
  t je parametar, 0 <= t <= 1
 *******************************************************/
 
  Point2D PointOnCubicBezier( Point2D* cp, float t )
  {
 	float   ax, bx, cx;
 	float   ay, by, cy;
 	float   tSquared, tCubed;
 	Point2D result;
 	
 	/* računa koeficijente polinoma*/
 	
 	cx = 3.0 * (cp[1].x - cp[0].x);
 	bx = 3.0 * (cp[2].x - cp[1].x) - cx;
 	ax = cp[3].x - cp[0].x - cx - bx;
 	
 	cy = 3.0 * (cp[1].y - cp[0].y);
 	by = 3.0 * (cp[2].y - cp[1].y) - cy;
 	ay = cp[3].y - cp[0].y - cy - by;
 	
 	/* računa tačku krive u zavisnosti od parametra t */
 	
 	tSquared = t * t;
 	tCubed = tSquared * t;
 	
 	result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
 	result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
 	
 	return result;
  }
 
 /*****************************************************************************
  Argument funkcije ComputeBezier je niz struktura Point2D sa tačkama krive 
  generisanim uz pomoć kontrolnih tačaka cp. Pozivalac mora da obezbedi dovoljno
  memorije za rezultat čija je veličina <sizeof(Point2D) * brojTačaka>
 ******************************************************************************/
 
  void	ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve )
  {
 	float dt;
 	int   i;
 	
 	dt = 1.0 / ( numberOfPoints - 1 );
 	
 	for( i = 0; i < numberOfPoints; i++ )
 		curve[i] = PointOnCubicBezier( cp, i*dt );
  }

Grafika

Bezjeove krive se naširoko koriste za modelovanje glatkih krivih. Afine transformacije kao što su translacija i rotacija mogu biti primenjene na kontrolne tačke krive.

Najčešće se koriste kvadratna i kubna kriva, jer krive većeg stepena troše mnogo više resursa računara daljom obradom. Kada su potrebni složeniji oblici, krive nižeg reda se spajaju i formiraju složenu Bezjeovu krivu, tzv. Bezjeov splajn. U jezicima vektorske grafike se složena Bezijerova kriva zove još i putanja. Kako bi se garantovala glatkoća krive, kontrolna tačka u kojoj se dve krive spajaju mora da bude na liniji između dve kontrolne tačke sa obe strane.

Standard za vektorsku grafiku naziva se -{SVG}-, a postoje programi za vektorsku grafiku: -{Adobe Illustrator}-, -{CorelDraw}-, -{Inkscape}-...

Najčešće korišćeni metod za rasterizovanje Bezjeove krive je rekurzivna podela, u kojoj se proveravaju kontrolne tačke, kako bi se otkrilo da li je kriva dovoljno glatka. U slučaju da nije, kriva se deli parametarski na dva segmenta i ista rekurzivna procedura se sprovodi nad oba dela.

Animacije

U -{Adobe Flash}- i -{Synfig}- animacijama, Bezijerove krive se koriste za konstruisanje. Recimo da korisnik želi da se njegov objekat kreće određenom putanjom. On će tu putanju zadati kao Bezjeovu krivu, a aplikacija će na osnovu unosa napraviti potrebne okvire po kojima će se objekat kretati.

Animacija Bezijerove krive u programskom jeziku -{Java}-

Animacija Bezjeove krive u programskom jeziku -{Python}-

Konstrukcija krivih

Linearne krive

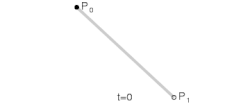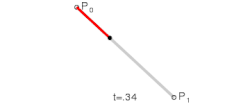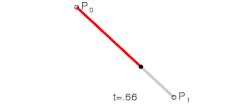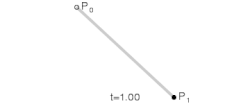
Parametar $t$ kod linearne Bezjeove krive može biti protumačen kao „koliko je $\alpha (t)$ daleko od $P_0$ krećući se ka $P_1$. Na primer, kada je $t=0.5$ , $\alpha (t)$ je na pola puta od $P_0$ ka $P_1$. Promenom parametra $t$ od 0 do 1, ispisuje se prava linija.

Animacija linearne Bezjeove krive, t je iz [0,1]

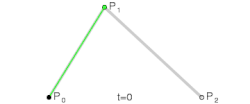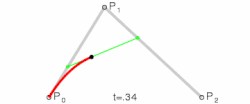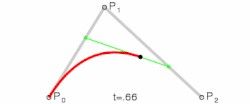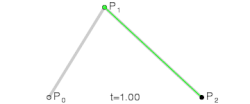
Kvadratne krive

Dok parametar $t$ varira od 0 do 1, moguće je uočiti sledeće:

• Tačku $Q_0(t)$ koja varira od $P_0$ do $P_1$ i time ispisuje linearnu Bezjeovu krivu
• Tačku $Q_1(t)$ koja varira od $P_1$ do $P_2$ i time ispisuje linearnu Bezjeovu krivu
• Tačku $\alpha (t)$ koja je linearna interpolacija tačaka $Q_0$ i $Q_1$ i time ispisuje kvadratnu Bezjeovu krivu

Konstrukcija kvadratne Bezjeove krive

Animacija kvadratne Bezjeove krive, t je iz [0,1]

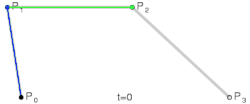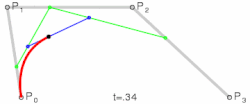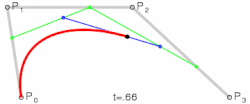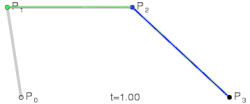
Krive višeg stepena

• Kubna Bezjeova kriva ima tri tačke $Q_0,Q_1,Q_2$ koje ispisuju linearne krive i tačke $R_0,R_1$ koje opisuju kvadratne Bezjeove krive.

Konstrukcija kubne Bezjeove krive

Animacija kubne Bezjeove krive, t je iz [0,1]

• Kriva stepena četiri ima četiri tačke za opis linearnih krivih, tri tačke koje opisuju kvadratne krive i dve tačke koje opisuju kubne Bezjeove krive.

Konstrukcija Bezjeove krive stepena 4

Animacija Bezjeove krive stepena 4, t je iz [0,1]

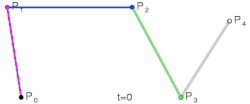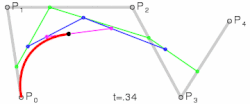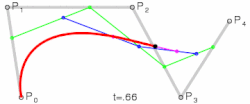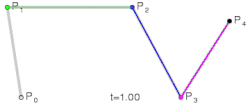• Analogijom konstruišemo i krivu petog stepena, kao i krive većih stepena

Animacija Bezijerove krive petog stepena

Literatura

• Шаблон:Cite book
• Шаблон:Cite book

Video snimci

• Animacija Bezijerovih krivih
• Animacija Bezijerovih krivih
• Crtanje hobotnice pomoću Bezijerovih krivih
• -{GeoGebra}-
• Bezijerove krive u -{PowerPoint}--u
• -{OpenGL}-
• Bezijerove krive u računarskoj grafici
• -{JavaScript}- tutorial za Bezijerove krive
• Splajnovi
• Mali čas Bezijerovih krivih
• Racionalne Bezijerove krive
• -{Inkscape}- tutorial
• -{Inkscape}- tutorial: nacrtati macu pomoću Bezijerovih krivih

Vidi još

• De-Kasteljau algoritam
• Geometrija
• Računarska grafika
• -{LaTeX}- priručnik na engleskom jeziku

Spoljašnje veze

• Animacija Bezijerovih krivih
• Bezijerove krive na -{WolframMathWorld}--u
• Od Bezijera do Bernštajna
• Programerski kodovi
• Programerski kodovi
• Matrična reprezentacija Bezijerovih krivih