Diferencijalni račun

Grafikon funkcije, nacrtan u crnom bojom, i tangenta te funkciju, nacrtana crvenom bojom. Nagib tangentne linije jednak je derivatu funkcije na označenoj tački.

U matematici, diferencijalni račun je podpolje računa koje se bavi proučavanjem stopa kojima se veličine menjaju. To je jedan od dva tradicionalna dela računa, pri čemu je drugi integralni račun, proučavanje područja ispod krive.

Primarni predmeti proučavanja u diferencijalnom računu su derivacija funkcije, srodni pojmovi kao što su diferencijali i njihove primene. Derivat funkcije pri izabranoj ulaznoj vrednosti opisuje brzinu promene funkcije u blizini te ulazne vrednosti. Proces pronalaženja derivata se naziva diferencijacija. Geometrijski, derivat u tački je nagib tangentne linije na grafikonu funkcije u toj tački, pod uslovom da derivat postoji i da je definisan u toj tački. Za funkciju realnih vrednosti jedne realne promenljive, derivat funkcije u tački generalno određuje najbolju linearnu aproksimaciju funkcije u toj tački. Diferencijalni račun i integralni račun su povezani fundamentalnim teoremom računa, koji navodi da je diferencijacija obrnuti proces integracije.

Diferencijacija nalazi primene u skoro svim kvantitativnim disciplinama. Na primer, u fizici, derivat pomeranja pokretnog tela u odnosu na vreme je brzina tela, a derivat brzine u odnosu na vreme je ubrzanje. Derivat momenta tela u odnosu na vreme jednak je sili primenjenoj na telo; preraspodela izraza ovog derivata dovodi do poznate jednačine Шаблон:Math, povezane sa Njutnovim drugim zakonom kretanja. Brzina hemijske reakcije je derivat. U operacionim istraživanjima, derivati određuju najefikasnije načine za transport materijala i dizajniranje fabrika.

Derivati se često koriste za pronalaženje maksimuma i minimuma funkcije. Jednačine koje uključuju derivate nazivaju se diferencijalne jednačine i fundamentalne su za opisivanje prirodnih fenomena. Derivati i njihove generalizacije pojavljuju se u mnogim oblastima matematike, kao što su kompleksna analiza, funkcionalna analiza, diferencijalna geometrija, teorija mera i apstraktna algebra.

Izvod

Tangetna linija u Шаблон:Math

Izvod raznih tačaka diferencijabilne funkcije

Pretpostavimo da su Шаблон:Math i Шаблон:Math realni brojevi i da je Шаблон:Math funkcija od Шаблон:Math, to jest, za svaku vrednost Шаблон:Math postoji odgovarajuća vrijednost Шаблон:Math. Ovaj odnos se može zapisati kao Шаблон:Math. Ako je Шаблон:Math jednačina za pravu liniju (zvana linearna jednačina), onda postoje dva realna broja Шаблон:Math i Шаблон:Math takva da je Шаблон:Math. U ovoj „formi nagiva i preseka”, izraz Шаблон:Math se naziva nagib i može se odrediti iz formule:

$m=\frac{\text{promena u }y}{\text{promena u }x}=\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x},$

gde je simbol Шаблон:Math (veliko grčko slovo delta) skraćenica za „promena u”. Odatle sledi da je Шаблон:Math.

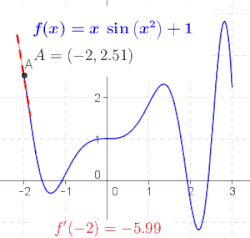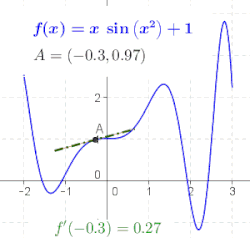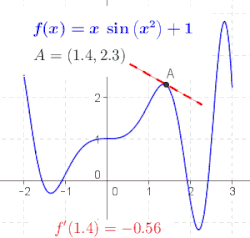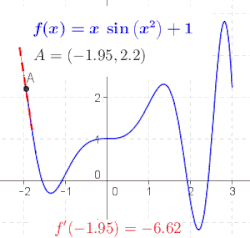
Generalna funkcija nije linija, tako da nema nagib. Geometrijski, izvod od Шаблон:Math u tački Шаблон:Math je nagib tangentne linije funkcije Шаблон:Math u tački Шаблон:Math (pogledajte sliku). To se često označava sa Шаблон:Math u Lagranžovoj notaciji ili Шаблон:Math u Lajbnicovoj notaciji. Kako je izvod nagib linearne aproksimacije od Шаблон:Math u tački Шаблон:Math, izvod (zajedno sa vrednošću Шаблон:Math u Шаблон:Math) određuje najbolju linearnu aproksimaciju, ili linearizaciju, od Шаблон:Math u blizini tačkie Шаблон:Math.

Ako svaka tačka Шаблон:Math u domenu funkcije Шаблон:Math ima izvod, onda postoji funkcija koja šalje svaku tačku Шаблон:Math u derivat od Шаблон:Math u Шаблон:Math. Na primer, ako je Шаблон:Math, onda je funkcija izvoda Шаблон:Math.

Blisko srodna notacije je diferencijal funkcije. Kad su Шаблон:Math i Шаблон:Math realne promenljive, derivat Шаблон:Math od Шаблон:Math je nagib tangetne linije na grafikonu Шаблон:Math od Шаблон:Math. Budući da su izvor i cilj funkcije Шаблон:Math jednodimenzionalni, derivat od Шаблон:Math je realni broj. Ako su Шаблон:Math i Шаблон:Math vektori, tada najbolja linearna aproksimacija grafu Шаблон:Math zavisi od toga kako se Шаблон:Math menja u više smerova odjednom. Uzimajući najbolju linearnu aproksimaciju u jednom pravcu, određuje se parcijalni derivat, koji se obično označava Шаблон:Math. Linearizacija Шаблон:Math u svim pravcima odjednom se naziva totalni derivat.

Literatura

• Шаблон:Cite book
• Larson, Ron, Bruce H. Edwards. "Calculus", 9th ed., Brooks Cole Cengage Learning. Шаблон:Page.
• Шаблон:Cite book
• Шаблон:Cite book
• Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano.. "Calculus", 11th ed., Addison-Wesley. Шаблон:Page.
• Courant, Richard. Шаблон:ISBN. Introduction to calculus and analysis 1.
• Edmund Landau. Шаблон:ISBN Differential and Integral Calculus, American Mathematical Society.
• Robert A. Adams. Шаблон:Page. Calculus: A complete course.
• Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7.
• Шаблон:Cite book Uses synthetic differential geometry and nilpotent infinitesimals.
• Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1–46.
• Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton University Press, 2004.
• Cliff Pickover. Шаблон:Page. Calculus and Pizza: A Math Cookbook for the Hungry Mind.
• Michael Spivak. (September 1994). Шаблон:ISBN. Calculus. Publish or Perish publishing.
• Tom M. Apostol. Шаблон:Page. Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.
• Tom M. Apostol. Шаблон:Page. Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.
• Silvanus P. Thompson and Martin Gardner. Шаблон:Page. Calculus Made Easy.
• Шаблон:Cite book, The Association, Stony Brook, NY. ED 300 252.
• Thomas/Finney. Шаблон:Page. Calculus and Analytic geometry 9th, Addison Wesley.
• Шаблон:Cite web From MathWorld—A Wolfram Web Resource.
• Crowell, B. (2003). "Calculus" Light and Matter, Fullerton., Приступљено 6. 5. 2007. from -{R|http://www.lightandmatter.com/calc/calc.pdf}-
• Garrett, P. (2006). "Notes on first year calculus" University of Minnesota. from Шаблон:Cite web
• Faraz, H. (2006). "Understanding Calculus", Приступљено 6. 5. 2007. from Understanding Calculus, URL -{R|http://www.understandingcalculus.com/}- (HTML only)
• Keisler, H. J. (2000). "Elementary Calculus: An Approach Using Infinitesimals" from Шаблон:Cite web
• Mauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. from Шаблон:Cite web
• Sloughter, Dan (2000). "Difference Equations to Differential Equations: An introduction to calculus"., Приступљено 17. 3. 2009. from -{R|http://synechism.org/drupal/de2de/}-
• Stroyan, K.D. (2004). "A brief introduction to infinitesimal calculus" University of Iowa., Приступљено 6. 5. 2007. from -{R|https://web.archive.org/web/20050911104158/http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm}- (HTML only)
• Strang, G. (1991). "Calculus" Massachusetts Institute of Technology., Приступљено 6. 5. 2007. from -{R|http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm}-
• Smith, William V. (2001). "The Calculus" [1] Шаблон:Wayback (HTML only).
• Шаблон:Cite book
• Шаблон:Cite journal
• Шаблон:Cite book Republication of a 1939 book (2nd printing in 1949) with a different title.
• Шаблон:Cite book
• Шаблон:Cite journal
• Grattan-Guinness, Ivor. The Rainbow of Mathematics: A History of the Mathematical Sciences, Chapters 5 and 6, W. W. Norton & Company, 2000.
• Hoffman, Ruth Irene, "On the development and use of the concepts of the infinitesimal calculus before Newton and Leibniz", Thesis (M.A.), University of Colorado, 1937

Spoljašnje veze

• Шаблон:Springer
• Шаблон:MathWorld
• Шаблон:PlanetMath
• Calculus Made Easy (1914) by Silvanus P. Thompson Full text in PDF
• Шаблон:In Our Time
• Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sites
• COW: Calculus on the Web Шаблон:Wayback at Temple University – contains resources ranging from pre-calculus and associated algebra
• Earliest Known Uses of Some of the Words of Mathematics: Calculus & Analysis
• Online Integrator (WebMathematica) from Wolfram Research
• The Role of Calculus in College Mathematics Шаблон:Wayback from ERICDigests.org
• OpenCourseWare Calculus Шаблон:Wayback from the Massachusetts Institute of Technology
• Infinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, ed. Michiel Hazewinkel.
• Шаблон:Cite web
• Calculus Problems and Solutions by D.A. Kouba
• Donald Allen's notes on calculus Шаблон:Wayback
• Calculus training materials at imomath.com Шаблон:Wayback