Podudarnost (geometrija)

Primer podudarnosti. Dva trougla levo su podudarna, dok je treći sličan njima. Zadnji trougao nije ni sličan ni podudaran sa ostalima. Podudarnost dozvoljava izmene nekih svojstava, kao što su lokacija i orijentacija, ali ostavlja ostale nepromenjenim, kao što su rastojanje i uglovi. Nepromenjena svojstva se nazivaju invarijantama.

Ovaj dijagram ilustruje geometrijski princip „ugao-ugao-strana” podudarnosti: Ako su dati trouglovi -{ABC}- i -{A'B'C'}-, trougao -{ABC}- je podudaran sa trouglom -{A'B'C'}- ako i samo ako je ugao -{CAB}- podudaran sa -{C'A'B'}- i ugao -{ABC}- je podudaran sa -{A'B'C'}-, i BC je podudarno sa -{B'C'}-

U geometriji dve figure su podudarne ako imaju istu veličinu i oblik, ili ako jedna ima isti oblik i veličinu kao slika u ogledalu druge. Dva skupa tačaka su podudarna ako postoji preslikavanje kojim se taj skup preslikava u drugi skup, a da se pri tom ne menja veličina i oblik.

Podudarnost se označava sa $\cong$

Podudaran ima značenje:

1. Dve duži su podudarne ako imaju istu dužinu $d_1=d_2$ tj $d_1\cong d_2$
2. Dva ugla su podudarna ako imaju istu meru ${\alpha }_1={\alpha }_2$ tj ${\alpha }_1\cong {\alpha }_2$
3. Dva kruga su podudarna ako imaju isti prečnik $R_1\cong R_2$ tj $R_1\cong R_2$

Određivanje podudarnosti poligona

Narandžasti i zeleni četvorougao su podudarni; plavi nije kongruentan sa njima. Sva tri imaju isti obim i površinu. (Redosled stranica plavog četvorougla je „pomešan“ što dovodi do toga da dva unutrašnja ugla i jedna od dijagonala nisu podudarni.)

Da bi dva poligona bila podudarna, moraju imati jednak broj stranica (a samim tim i jednak broj – isti broj – temena). Dva poligona sa n strana su podudarna ako i samo ako svaki od njih ima numerički identične nizove (čak i ako u smeru kazaljke na satu za jedan poligon i suprotno od kazaljke na satu za drugi) stranica-ugao-stranica-ugao- ... za n stranica i n uglova.

Kongruencija poligona može se grafički utvrditi na sledeći način:

• Prvo, uparite i označite odgovarajuće vrhove dve figure.
• Drugo, nacrtajte vektor od jednog od vrhova jedne od figura do odgovarajućeg temena druge figure. Translirajte prvu figuru ovim vektorom tako da se ova dva temena poklapaju.
• Treće, rotirajte transliranu figuru oko podudarnog temena dok se jedan par odgovarajućih strana ne poklopi.
• Četvrto, odrazite rotiranu figuru oko ove uparene strane dok se brojke ne poklope.

Ako u bilo kom trenutku korak ne može da se završi, poligoni nisu podudarni.

Aksiomi podudarnosti

Aksiomi podudarnosti opisuju osnovne karakteristike relacije podudarnosti parova tačaka. Ovu relacija se uvodi kao polazni pojam.

• Aksiom 1

Ako je $(A,B)\cong (C,D)$ i $A=B$, tada je i $C=D$.

• Aksiom 2

Za svake dve tačke $A$ i $B$ je $(A,B)\cong (B,A)$.

• Aksiom 3

Ako je $(A,B)\cong (C,D)$ i $(A,B)\cong (E,F)$ tada je $(C,D)\cong (E,F)$

• Aksiom 4

Ako su -{C}- i -{C'}- tačke otvorenih duži -{AB}- i -{A'B'}-, takve da je $(A,C)\cong (A^{\prime },C^{\prime })$ i $(B,C)\cong (B^{\prime },C^{\prime })$, tada je i $(B,C)\cong (A^{\prime },B^{\prime })$

• Aksiom 5

Ako su -{A}- i -{B}- dve tačke i -{CX}- poluprava tada na toj polupravoj postoji tačka -{D}- takva da je $(A,B)\cong (C,D)$

• Aksiom 6

Ako su -{A, B, C}- tri nekolinearne tačke i $A^{\prime },B^{\prime }$ tačke ruba neke poluravni $\pi$, takve da je $(A,B)\cong (A^{\prime },B^{\prime })$ tada u toj poluravni postoji jedinstvena tačka -{C'}- takva da je $(A,C)\cong (A^{\prime },C^{\prime })$ i $(B,C)\cong (B^{\prime },C^{\prime })$

• Aksiom 7

Ako su -{A, B, C}- i -{A', B', C'}- dve trojke nekolinearnih tačaka i -{D}- i -{D'}- tačke polupravih -{BC}- i -{B'C'}- takve da je $(AB)\cong (A^{\prime },B^{\prime })$ , $(BC)\cong (B^{\prime },C^{\prime })$, $(A,C)\cong (A^{\prime },C^{\prime })$ i $(B,D)\cong (B^{\prime },D^{\prime })$, tada je i $(A,D)\cong (A^{\prime },D^{\prime })$

Relacija podudarnosti parova tačaka je relacija ekvivalencije.

1. $(A,B)\cong (A,B)$ relacija je refleksivna.
2. Neka je $(AB)\cong (C,D)$ [$(A,B)\cong (A,B)$] => $(CD)\cong (A,B)$ relacija je simetrična
3. $(A,B)\cong (C,D)$ i $(C,D)\cong (E,F)=>$ $(A,B)\cong (E,F)$ [sledi na osnovu simetričnosti]

Teorema 1

Ako su -{A}- i -{B}- dve tačke i -{CX}- poluprava tada na toj polupravoj postoji jedinstvena tačka -{D}- takva da je '$(A,B)\cong (CD)$

Teorema 2

Ako su -{A,B,C}- tri razne tačke prave -{p}- i -{A',B'}- dve tačke prave -{p'}- takve da je $(A,B)\cong (A^{\prime },B^{\prime })$, tada postoji jedinstvena tačka -{C'}- takva da je -{A',B'}- i $(A,C)\cong (A^{\prime },C^{\prime })$.

Pri tome, tačka -{C'}- pripada pravoj -{p'}- i:

1. ako je $𝔅(A,C,B)$, tada je $𝔅(A^{\prime },C^{\prime },B^{\prime })$
2. ako je $𝔅(A,B,C)$, tada je $𝔅(A^{\prime },B^{\prime },C^{\prime })$
3. ako je $𝔅(B,C,A)$, tada je $𝔅(B^{\prime },C^{\prime },A^{\prime })$

Definicija 1

Kaže se da je uređena -{n}--torka tačaka $(A_1,A_2,...,A_n)$ podudarna sa -{n}--torkom $(A{\text{'}}_1,A{\text{'}}_2,...,A{\text{'}}_n)$ u oznaci $(A_1,A_2,...,A_n)\cong (A{\text{'}}_1,A{\text{'}}_2,...,A{\text{'}}_n)$

ako je za svako $(i,k)\in \left\{\begin{array}{c}1,2,...n\end{array}\right\}(A_i,A_k)\cong (A{\text{'}}_i,A{\text{'}}_k)$

Definicija 2

Neka su A i -{B}- dve razne tačke neke ravni $\alpha$. Skup svih tačaka $X$ te ravni takvih da je $(A,B)\cong (A,X)$, naziva se krug, u oznaci $k(A,AB)$, sa centrom A i čiji je poluprečnik duž -{AB}-.

Podudarnost duži

Ako su dve duži -{AB}- i -{CD}- su podudarne, to može se označiti sa $AB\cong CD$

Teorema 3

$(A,B)\cong (A^{\prime },B^{\prime })=>A,B\cong A^{\prime },B^{\prime }$,

Definicija 3

Tačka -{S}- je središte duži $AB$, ako pripada toj duži i važi $AS\cong SB$

Teorema 4

Za svaku duž postoji jedinstveno središte.

Definicija 4

Duž -{AB}- je manja od duži -{CD}- u oznaci -{AB < CD}- ako unutar duži -{CD}- postoji tačka -{E}- takva da je -{AB ≅ CE}-. Takođe u tom slučaju se kaže i da je duž -{CD}- veća od duži -{AB}- u oznaci -{CD > AB}-.

Definicija 5

Duž -{EF}- jednaka je zbiru duži -{AB}- i -{CD}- u oznaci -{EF = AB + CD}-, ako unutar duži -{EF}- postoji tačka -{G}- takva da je -{AB≅EG CD ≅GF}-.

Na isti način definišu se razlika, proizvod duži i prirodnog broja, proizvod duži iracionalnog broja

Podudarnost uglova, pravi uglovi, relacija normalnosti pravih

Dva konveksna ili konkavna ugla $pOq$ i $p_1{O}_1{q}_1$ su podudarna ako i samo ako na kracima $p$ i $q$ $p_1$, $q_1$ redom postoje tačke $P,Q,P_1,Q_1$ takve da je: $(P,O,Q)\cong (P_1,O_1,Q_1$).

Teorema 5

• Unakrsni uglovi su međusobno podudarni.
• Za svaki -{∠pq}- i svaku polupravu -{p'}- neke ravni, postoji u poluravni određenoj pravom koja sadrži -{p'}-, jedinstvena poluprava -{q'}- takva da -{∠pq ≅ ∠p'q'}-.

Teorema 6

Svaki ugao ima jedinstvenu bisektrisu

Definicija 5

Ugao -{AOB}- je manji od ugla -{CSD}- u oznaci $\mathrm{\angle }AOB<\mathrm{\angle }CSD$ ako unutar ugla -{CSD}- postoji poluprava -{SE}- takva da je $\mathrm{\angle }AOB\cong \mathrm{\angle }CSE$. U tom slučaju kažemo ia je ugao -{CSD}- veći od ugla -{AOB}- u oznaci $\mathrm{\angle }CSD>\mathrm{\angle }AOB$.

Definicija 6

Uglom dve mimoilazne prave -{p}- i -{q}- u prostoru $E^3$ naziva se ugao koji određuju njima paralelne prave -{a}- i -{b}- koje se seku u nekoj tački O. Specijalno, ako je ugao dve mimoilazne prave u prostoru $E^3$ prav, tada se kaže da su prave $p$ i $q$ normalne među sobom, i simbolički označavamo sa $p\perp q$

Teorema 7

1. Ugao podudaran nekom pravom uglu takođe je prav.
2. Pravi uglovi su među sobom podudarni.
3. Postoji jedna i samo jedna prava koja seče svaku od dve mimoilazne prave -{a}- i -{b}- pod pravim uglom.

Podudarnost poligona

Iako sva tri poligona imaju isti obim i površinu podudarni su samo narandžasti i zeleni

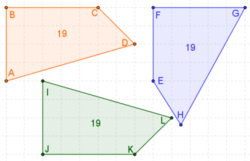
Dva podudarna poligona imaju isti broj stranica i vrhova.

Dva poligoni sa -{n}- strana su podudarna, ako i samo ako svaki od njih ima odgovarajuće stranice i uglove jednake.

Podudarnost nekih pravilnih četvorouglova

1. Dva paralelograma su podudarna ako su im podudarne dve susedne ivice i jedan ugao.
2. Dva pravougaonika su podudarna ako su im podudarne dve susedne ivice.
3. Dva romba su podudarna ako su im podudarne jedna ivica i jedan ugao
4. Dva kvadrata su podudarna ako su im podudarne stranice.

Podudarnost trouglova

Podudarnost trouglova

Dva trougla su podudarna ako su njihove odgovarajuće stranice jednake dužine, odgovarajući uglovi jednake veličine. Da su dva trougla -{ABC}- i -{DEF}- podudarni zapisuje se

$\mathrm{△}\mathrm{A}\mathrm{B}\mathrm{C}\cong \mathrm{△}\mathrm{D}\mathrm{E}\mathrm{F}$

Određivanje podudarnosti

• SUS

Dva trougla su podudarna ako su dve ivice i njima zahvaćeni ugao jednog trougla podudarni sa odgovarajućim ivicama i uglovima drugog trougla, tj: $AB\cong A^{\prime }{B}^{\prime },AC\cong A^{\prime }{C}^{\prime },\mathrm{\angle }BAC\cong \mathrm{\angle }{B}^{\prime }{A}^{\prime }{C}^{\prime }=>\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$

• SSS

Dva trougla su podudarna ako su im odgovarajuće ivice podudarne, tj. $AB\cong A^{\prime }{B}^{\prime },BC\cong B^{\prime }{C}^{\prime },AC\cong A^{\prime }{C}^{\prime }=>\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$

Dokaz:

Neka su -{ABC, A'B'C'}- dva trougla takva da je $AB\cong A^{\prime }{B}^{\prime },BC\cong B^{\prime }{C}^{\prime },AC\cong A^{\prime }{C}^{\prime }$. Tada su i odgovarajući parovi tačaka podudarni tj. $\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }.$

Postoji izometrija te ravni, koja tačke -{A,B,C}- preslikava redom u tačke -{A', B', C'.}- Izometrije čuvaju raspored, pa se odgovarajuće ivice jednog trougla preslikavaju u odgovarajuće ivice drugog trougla. Izometrija preslikava trougao -{ABC}- u trougao -{A'B'C'}-, pa je $\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }.$

• USU

Dva trougla su podudarna ako su jedna ivica i na njoj nalegli uglovi jednog trougla podudarni sa odgovarajućom ivicom i odgovarajućim uglovima drugog trougla, tj: $BC\cong B^{\prime }{C}^{\prime },\mathrm{\angle }ABC\cong \mathrm{\angle }{A}^{\prime }{B}^{\prime }{C}^{\prime },\mathrm{\angle }ACB\cong \mathrm{\angle }{A}^{\prime }{C}^{\prime }{B}^{\prime }=>\mathrm{△}ABC\cong \mathrm{△}{A}^{\prime }{B}^{\prime }{C}^{\prime }$

• SSU

Dva trougla su podudarna ako su dve ivice i ugao naspram jedne od njih jednog trougla podudarni sa odgovarajućim stranicama i odgovarajućim uglom drugog trougla.

Literatura

• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Nikolai I. Lobachevsky, Pangeometry, translator and editor: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society, 2010.
• Jay Kappraff, A Participatory Approach to Modern Geometry, World Scientific Publishing. Шаблон:Page.
• Leonard Mlodinow, Euclid's Window – The Story of Geometry from Parallel Lines to Hyperspace, UK edn. Allen Lane, 1992.
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Judith N. Cederberg (1989, 2001) A Course in Modern Geometries, Chapter 3.12 Similarity Transformations, pp. 183–9, Springer. Шаблон:Page .
• Günter Ewald (1971) Geometry: An Introduction, pp. 106, 181, Wadsworth Publishing.
• George E. Martin (1982) Transformation Geometry: An Introduction to Symmetry, Chapter 13 Similarities in the Plane, pp. 136–46, Springer. Шаблон:Page .

Spoljašnje veze

• Geometrija
• -{The SSS at Cut-the-Knot}-
• -{The SSA at Cut-the-Knot}-
• -{Interactive animations demonstrating Congruent polygons, Congruent angles, Congruent line segments, Congruent triangles at Math Open Reference}-