Фарадејев закон електромагнетске индукције

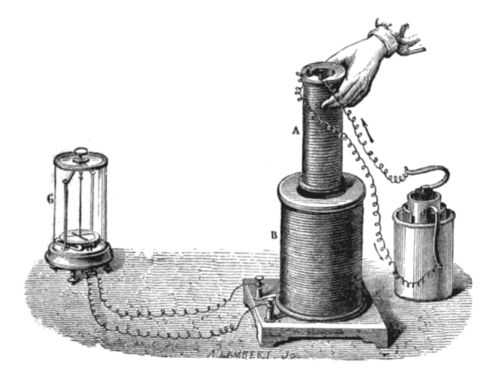
Фарадејев експеримент који показује индукцију између намотаја жице: Течна батерија (десно) даје струју која протиче кроз малу завојницу (-{A}-), стварајући магнетно поље. Када су завојнице непомичне, не индукује се струја. Али када се мала завојница помери унутар или ван велике завојнице (-{B}-), магнетни ток кроз велику завојницу се мења, изазивајући струју коју детектује галванометар (-{G}-).

Фарадејев закон електромагнетске индукције (скраћено, Фарадејев закон) је основни закон електромагнетизма који предвиђа како ће магнетно поље ступити у интеракцију са електричним колом да би произвело електромоторну силу (ЕМС) - феномен познат као електромагнетна индукција. То је основни принцип рада трансформатора, индуктора и многих врста електромотора, генератора и соленоида.

Фарадејев закон електромагнетске индукције даје однос промене магнетског флукса кроз површину $S$ ограниченом контуром $C$ и електричног поља дуж те контуре:

${\oint }_{C}E\cdot dl=-\frac{d}{dt}\underset{S}{\int }B\cdot dS$

где је $E$ електрично поље, $dl$ је инфинитезимални елемент контуре $C$ и $B$ је густина магнетског флукса. Смер контуре $C$ и $dS$ одређују се правилом десне руке.

Еквивалентно, диференцијални облик Фарадејевог закона је:

$\mathrm{\nabla }\times E=-\frac{\partial B}{\partial t}$

што је једна од Максвелових једначина.

У случају калема где проводници сачињавају $N$ навојака, израз постаје:

$V=-N\frac{d\mathrm{\Phi }}{dt}$

где је $V$ индукована електромоторна сила а $\frac{d\mathrm{\Phi }}{dt}$ је брзина промене у времену магнетног флукса $\mathrm{\Phi }$. Смер електромоторне силе (негативан знак у изразу) је први пут дата Ленцовим законом. Фарадејев закон, заједно са осталим законима електромагнетизма, је касније уграђен у Максвелове једначине. Фарадејев закон је заснован на Мајкл Фарадејевим експериментима 1831.

Историја

Дијаграм Фарадејевог апарата са гвозденим прстеном. Променљиви магнетни флукс леве завојнице изазива струју у десној завојници.

Електромагнетну индукцију независно су открили Мајкл Фарадеј 1831. и Џозеф Хенри 1832. Фарадеј је први објавио резултате својих експеримената. У првој Фарадејевој експерименталној демонстрацији електромагнетне индукције (29. августа 1831), он је омотао две жице око супротних страна гвозденог прстена (торус) (распоред сличан савременом тороидном трансформатору). На основу своје процене недавно откривених својстава електромагнета, очекивао је да ће, када струја почне да тече у једној жици, нека врста таласа проћи кроз прстен и изазвати неки електрични ефекат на супротној страни. Он је повезао једну жицу са галванометром и посматрао док је другу жицу повезивао са батеријом. Он је уочио пролазну струју (коју је назвао „талас електричне енергије”) када је спојио жицу на батерију, а другу када ју је искључио.Шаблон:Rp Ова индукција је настала услед промене у магнетном флуксу до чега је дошло када је батерија прикључена и искључена. У року од два месеца, Фарадеј је открио неколико других манифестација електромагнетне индукције. На пример, уочио је пролазне струје када је брзо увукао и извукао штапни магнет у жичану завојницу, и генерисао је сталну (једносмерну) струју ротирајући бакарни диск у близини магнета са клизним електричним проводником („Фарадејев диск").Шаблон:Rp

Фарадејев диск, први електрични генератор, тип хомополарног генератора.

Мајкл Фарадеј је објаснио електромагнетну индукцију користећи концепт који је назвао линије силе. Међутим, тадашњи научници су увелико одбацивали његове теоријске идеје, углавном зато што нису биле математички формулисане.Шаблон:Rp Изузетак је био Џејмс Клерк Максвел, који је 1861–62 користио Фарадејеве идеје као основу своје квантитативне електромагнетне теорије.Шаблон:Rp У Максвеловим радовима временски променљиви аспект електромагнетне индукције изражен је као диференцијална једначина коју је Оливер Хевисајд назвао Фарадејевим законом, иако се разликује од оригиналне верзије Фарадејевог закона, и не описује покретну електромагнетну силу. Хевисајдова верзија (погледајте Максвел–Фарадејову једначину испод) је облик који је данас препознат у групи једначина познатих као Максвелове једначине.

Ленцов закон, који је формулисао Емил Ленц 1834. године, описује „флукс кроз коло” и даје смер индуковане електромагнетне силе и струје настале услед електромагнетне индукције (разрађено у доњим примерима). Шаблон:Clear

Фарадејов закон

Наизменична електрична струја протиче кроз соленоид са леве стране, стварајући променљиво магнетно поље. Ово поље узрокује, електромагнетском индукцијом, електричну струју која тече у жичаној петљи са десне стране.

Најраширенија верзија Фарадаиевог закона наводи:Шаблон:Quotation

Математички исказ

Дефиниција површинског интеграла ослања се на цепање површине Шаблон:Math на мале површинске елементе. Сваки елемент је повезан са вектором Шаблон:Math величине једнаке површини елемента и са правцем нормалним на елемент и усмереним „према споља” (у односу на оријентацију површине).

За петљу жице у магнетном пољу, магнетни флукс Шаблон:Math је дефинисан за било коју површину Шаблон:Math чија је граница дата петљом. Пошто је могуће да се жичана петља креће, за површину се пише Шаблон:Math. Магнетски ток је површински интеграл:

${\mathrm{\Phi }}_B=\underset{\mathrm{\Sigma }(t)}{\iint }𝐁(t)\cdot \mathrm{d}𝐀,$

где је Шаблон:Math елемент покретне површине Шаблон:Math, Шаблон:Math је магнетно поље, а Шаблон:Math је скаларни производ вектора који представља елемент флукса кроз Шаблон:Math. Визуелно гледано, магнетни флукс кроз жичану петљу сразмеран је броју линија магнетног поља које пролазе кроз петљу.

Када се флукс промени - због промене Шаблон:Math, или због померања или деформације жичане петље, или оба - Фарадејев закон индукције наводи да жичана петља добија ЕМС, дефинисану као енергију доступну из јединичног набоја који је једном путовао око жичане петље.Шаблон:Rp (Неки извори наводе дефиницију другачије. Овај израз је изабран ради компатибилности са једначинама специјалне релативности.) Еквивалентно, то је напон који би се мерио пресецањем жица за стварање отвореног кола, и причвршћеног волтметра на електроде.

Фарадејев закон наводи да је ЕМС такође одређена брзином промене магнетног флукса:

$ℰ=-\frac{\mathrm{d}{\mathrm{\Phi }}_B}{\mathrm{d}t},$

где је $ℰ$ електромоторна сила (ЕМС) а Шаблон:Math је магнетски флукс.

Смер електромоторне силе дат је Ленцовим законом.

Законе индукције електричних струја у математичком облику установио је Франц Ернст Нојман 1845.

Види још

• Индукција
• Електромагнетизам
• Магнетско поље
• Електрично поље
• Густина магнетског флукса
• Максвелове једначине
• Мајкл Фарадеј
• Амперов закон

Литература

• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book (The relativity of magnetic and electric fields)
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book

Спољашње везе

• A simple interactive tutorial on electromagnetic induction (click and drag magnet back and forth) National High Magnetic Field Laboratory
• Roberto Vega. Induction: Faraday's law and Lenz's law – Highly animated lecture, with sound effects, Electricity and Magnetism course page
• Notes from Physics and Astronomy HyperPhysics at Georgia State University
• Tankersley and Mosca: Introducing Faraday's law
• A free simulation on motional EMF