Изохорски процес

Шаблон:Термодинамика Изохорски процес је термодинамички процес током којег запремина идеалног гаса који у њему учествује остаје константном.

Шарлов закон

Шаблон:Посебан чланак Приликом овог процеса важи следећа релација: -{p/T=const}-, што се изводи из једначине стања идеалног гаса. С обзиром да је -{pV=nRT}- => -{p/T=nR/V}-. Пошто су све величине са десне стране једнакости константне то важи и за целу десну страну па отуда добијамо наведену релацију између температуре и притиска при изохорском процесу.

Изохора

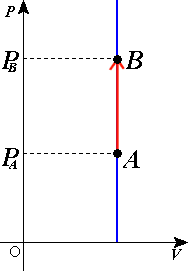
Овај процес можемо графички да представимо уз помоћ изохоре. У pV дијаграму има облик праве линије правца нормалног на -{V}--осу. На слици је приказана једна таква изохора. У том случају гас прелази из стања са мањим притиском у стање са већим. Пошто је изотерма која пролази кроз тачку која одговара коначном стању у овом процесу изнад оне која пролази кроз тачку која одређује почетно она одговара већој температури. Из тога се може закључити да је повећањем притиска дошло до пораста температуре, што је потврда важења Шарловог закона.

Изохора

Рад при изохорском процесу

При изохорском процесу гас не врши рад. То се може показати из релације:

$\mathrm{\Delta }W=p\mathrm{\Delta }V$

Пошто при изохорском процесу не долази до промене запремине важи да је ΔV једнако нули, отуда је и рад у овом процесу такође једнак нули.

Ово се може објаснити и преко дијаграма са слике. Рад је по дефиницији једнак површини испод графика датог процеса у pV дијаграму. Очигледно да је у овом случају та површина, а самим тим и рад једнаки нули.

Количина топлоте

Образац за количину топлоте ослобођене или добијене од стране система који учествује у изохорском процесу гласи:

$Q=n{C}_v\mathrm{\Delta }T$

Притом је: -{Q}-- тражена количина топлоте, -{n}-- број молова гаса који учествује у процесу ,-{c}--моларни топлотни капацитет при сталној запремини, -{Т}--температура.

Према Првом закону термодинамике:

$dU=dQ-dW$

С обзиром да је рад једнак нули:

$dU=dQ$

Како је $C_v=\frac{dU}{dT}$ за један мол гаса, за n мола важи:

$dQ=n{C}_{v}dT$

Интегралисањем обе стране добија се:

$Q=n\underset{T_1}{\overset{T_2}{\int }}CdT.$,

Или у коначном облику:

$Q=n{C}_v\mathrm{\Delta }T$

Види још

• Изотермски процес
• Изобарски процес
• Адијабатски процес
• Идеални гас

Спољашње везе

• -{Isochoric process}- Шаблон:En