Дефиниције непрекидности

Кошијева дефиниција

Илустровани приказ Кошијеве ε - δ дефиниције непрекидности. За нпр. ε=0.5, c=2, вредност δ=0.5 задовољава услов дефиниције.

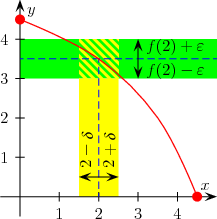
Дефиницију на $\epsilon -\delta$ језику је дао Коши и та дефиниција је везана је за функције реалних бројева.

Посматрајмо функцију $f:X\to ℝ,X\subseteq ℝ$. Нека је $x_0\in X$ тачка нагомилавања скупа $X$.

Функција $f$ је непрекидна у тачки $x_0$, ако је:

$(\mathrm{\forall }\epsilon >0)(\mathrm{\exists }\delta >0)(\mathrm{\forall }x\in X)(|x-x_0|<\delta \Rightarrow |f(x)-f(x_0)|<\epsilon )$

Ова дефиниција је еквивалентна са:

Функција $f$ је непрекидна у тачки $x_0$, ако је:

$\underset{x\to x_0}{lim}f(x)=f(x_0)$

Хајнеова дефиниција

Овом дефиницијом непрекидну функцију je Хајне дао преко граничне вредности низа.

Реална функција $f$ је непрекидна ако за сваки низ $(x_n{)}_{n\in \mathbb{N}}$, такав да

$\underset{n\to \mathrm{\infty }}{lim}{x}_n=L$,

важи

$\underset{n\to \mathrm{\infty }}{lim}f(x_n)=f(L)$

Овде смо наравно претпоставили да сваки члан низа припада домену функције.

Тополошка дефиниција

Функција $f:X\to ℝ$ је непрекидна у тачки $x_0\in X$ ако:

$(\mathrm{\forall }V\in 𝒱(f(x_0)))(\mathrm{\exists }U\in 𝒱(x_0))(f(U\cap X)\subseteq V)$

За функцију између два тополошка простора се каже да је непрекидна ако она сваки отворени инверзни скуп пресликава у отворени скуп.

Дефиниција непрекидности са стране

Функција непрекидна с десне стране

Посматрајмо функцију $f:X\to ℝ$,

функција је непрекидна са леве стране у тачки $x_0$ ако

$\underset{x\to x_0-0}{lim}f(x)=f(x_0)$

функција је непрекидна са десне стране у тачки $x_0$ ако

$\underset{x\to x_0+0}{lim}f(x)=f(x_0)$

Теорема: Функција $f:X\to ℝ$ је непрекидна у тачки $x_0\in X$ ако и само ако је непрекидна у тој тачки и са леве и са десне стране.

Види још

• Непрекидна функција
• Непрекидност
• Дефиниција

Литература

• Душан Аднађевић, Зоран Каделбург: Математичка анализа 1, Студентски трг, Београд, 1995.