Paretova raspodela

Paretova raspodela je imenovana po italijanskom građevinskom inženjeru, ekonomisti, i sociologu Vilfredu Paretu. Ona je raspodela verovatnoće stepenog zakona koja se koristi za opisivanje društvenih, naučnih, geofizičkih, aktuarskih, i mnogih drugih tipova uočljivih pojava. Prvobitno primenjena na opisivanje raspodele bogatstva u društvu, ona opisuje trend da veliki deo bogatstva poseduje mali deo stanovništva. Paretova distribucija je kolokvijalno postala poznata i naziva se Paretov princip, ili „80-20 pravilo”, a ponekad se naziva i „Matejev princip”. Ovo pravilo postulira da, na primer, 80% bogatstva društva drži 20% njegovog stanovništva. Međutim, ne treba poistovećivati Paretovu distribuciju i Paretov princip, jer distribucija daje ovaj rezultat samo za određenu vrednost stepena, $\alpha$ (α = log₄5 ≈ 1.16). Iako je $\alpha$ varijabilno, empirijskim opažanjima je ustanovljeno da 80-20 distribucija odgovara širokom rasponu slučajeva, uključujući prirodne pojave i ljudske aktivnosti.

Definicija

Ako je X randoman promenljiva sa Paretovom distribucijom (tip -{I}-), onda je verovatnoća da je X veće od nekog broja x, i.e. the funkcija preživljavanja (takođe zvana funkcija repa), data sa

$\bar{F}(x)=\mathrm{Pr}(X>x)=\{\begin{array}{cc}{\left(\frac{x_{\mathrm{m}}}{x}\right)}^{\alpha }& x\ge x_{\mathrm{m}},\\ 1& x<x_{\mathrm{m}},\end{array}$

gde je x_m (neophodno pozitivni) minimum moguće vrednosti od X, i α je pozitivni parameter. Paretova raspodela tipa -{I}- je karakterisana parametrom skaliranja x_m i parametrom oblika α, koji je poznat kao indeks repa. Kada se ova raspodela koristi za modelovanje raspodele bogatstva, onda se parameter α naziva Paretov indeks.

Svojstva

Funkcija kumulativne distribucije

Po definiciji, kumulativna funkcija raspodele Paretove randomne promenljive sa parametrima α i -{x_m}- je

$F_X(x)=\{\begin{array}{cc}1-{\left(\frac{x_{\mathrm{m}}}{x}\right)}^{\alpha }& x\ge x_{\mathrm{m}},\\ 0& x<x_{\mathrm{m}}.\end{array}$

Funkcija gustine verovatnoće

Po diferencijaciji sledi da je funkcija gustine verovatnoće

$f_X(x)=\{\begin{array}{cc}\frac{\alpha x_{\mathrm{m}}^{\alpha }}{x^{\alpha +1}}& x\ge x_{\mathrm{m}},\\ 0& x<x_{\mathrm{m}}.\end{array}$

Kada se prikaže na linearnim osama, distribucija pretpostavlja poznatu krivu u obliku slova J koja se asimptotski približava svakoj od ortogonalnih osa. Svi segmenti krive su slični (podložni odgovarajućim faktorima skaliranja). Kada je prikaže na log-log grafu, distribucija je predstavljena pravom linijom.

Momenti i karakteristična funkcija

• Očekivana vrednost randomne promenljive koja sledi Paretovu distribuciju je

$\mathrm{E}(X)=\{\begin{array}{cc}\mathrm{\infty }& \alpha \le 1,\\ \frac{\alpha x_{\mathrm{m}}}{\alpha -1}& \alpha >1.\end{array}$

• Varijansa randomne promenljive koja sledi Paretovu distribuciju je

$\mathrm{Var}(X)=\{\begin{array}{cc}\mathrm{\infty }& \alpha \in (1,2],\\ {\left(\frac{x_{\mathrm{m}}}{\alpha -1}\right)}^2\frac{\alpha }{\alpha -2}& \alpha >2.\end{array}$

(Ako je α ≤ 1, varijansa ne postoji.)

• Momenti su

${{\mu }_n}^{\prime }=\{\begin{array}{cc}\mathrm{\infty }& \alpha \le n,\\ \frac{\alpha x_{\mathrm{m}}^n}{\alpha -n}& \alpha >n.\end{array}$

• Momenat generisanja funkcije je definisan samo za nepozitivne vrednosti -{t}- ≤ 0

$M(t;\alpha ,x_{\mathrm{m}})=\mathrm{E}\left[e^{tX}\right]=\alpha (-x_{\mathrm{m}}t{)}^{\alpha }\mathrm{\Gamma }(-\alpha ,-x_{\mathrm{m}}t)$

$M(0,\alpha ,x_{\mathrm{m}})=1.$

• Karakteristična funkcija je data izrazom

$\phi (t;\alpha ,x_{\mathrm{m}})=\alpha (-i{x}_{\mathrm{m}}t{)}^{\alpha }\mathrm{\Gamma }(-\alpha ,-i{x}_{\mathrm{m}}t),$

gde je Γ(a, x) nekompletna gama funkcija.

Uslovne distribucije

Distribucija uslovne verovatnoće Pareto-raspodeljene randomne promenljive, datog događaja koji je veći ili jednak od zadatog broja $x_1$ do $x_{\text{m}}$, je Paretova distribucija sa istim Paretovim indeksom $\alpha$ ali sa minimumom $x_1$ umesto $x_{\text{m}}$.

Karakterizaciona teorema

Neka su $X_1,X_2,X_3,\dots$ nezavisne identično raspoređene randomne promenljive čija je raspodela verovatnoće podržana na intervalu $[x_{\text{m}},\mathrm{\infty })$ za neko $x_{\text{m}}>0$. Neka su za svako $n$, dve randomne promenljive $\min \{X_1,\dots ,X_n\}$ i $(X_1+\cdots +X_n)/\min \{X_1,\dots ,X_n\}$ nezavisne. Onda je zajednička distribucija Paretova distribucija.

Geometrijska sredina

Geometrijska sredina (-{G}-) je

$G=x_{\text{m}}\exp \left(\frac{1}{\alpha }\right).$

Harmonijska sredina

Harmonijska sredina (-{H}-) je

$H=x_{\text{m}}(1+\frac{1}{\alpha }).$

Primene

Vilfredo Pareto je izvorno koristio ovu distribuciju kako bi opisao raspodelu bogatstva među pojedincima, jer se činilo da prilično dobro pokazuje način na koji veći deo bogatstva bilo kog društva poseduje manji procenat ljudi u tom društvu. Takođe je koristio ovu distribuciju da opiše raspodelu dohotka. Ta se ideja ponekad izražava jednostavnije kao Paretov princip ili „pravilo 80-20”, što govori da 20% stanovništva kontroliše 80% bogatstva. Međutim, pravilo 80-20 odgovara određenoj vrednosti α, i zapravo, Paretovi podaci o britanskim porezima na dohodak u njegovom radu -{Cours d'économie politique}- pokazuju da je oko 30% stanovništva imalo oko 70% prihoda. Graf funkcije gustine verovatnoće (PDF) na početku ovog članka pokazuje da je „verovatnoća” ili deo populacije koja poseduje malu količinu bogatstva po osobi prilično visoka, a zatim se stalno smanjuje kako bogatstvo raste. (Paretova raspodela nije realistična za bogatstvo pri donjem kraju. Zapravo neto vrednost može čak da bude i negativna.) Ova distribucija nije ograničena na opisivanje bogatstva ili prihoda, već se susreće u mnogim situacijama u kojima je ravnoteža pronađena u distribuciji „malog” na „veliko”. Sledeći primeri se ponekad smatraju približno raspodeljenim po Paretovoj distribuciji:

Kumulativna Paretova (Lomaksova) distribucija do maksimalnih jednodnevnih padavina prikazana koristeći -{CumFreq}-

• Veličine ljudskih naselja (nekoliko gradova, mnogo zaseoka/sela)
• Raspodela veličina datoteka u Internet prometu koji koristi TCP protokol (mnogo manjih datoteka, nekoliko većih)
• Stope grešaka tvrdih diskova
• Klasteri Boze–Ajnštajnovog kondenzata u blizini apsolutne nule
• Vrednosti naftnih rezerivi u naftnim poljima (nekoliko velikih polja, mnogo malih polja)
• Рaspodela dužine poslova zadatih superračunarima (nekoliko velikih, puno malih)
• Standardizovane cene povraćaja na individualnim deonicama
• Veličine čestica peska
• Veličina meteorita
• Ozbiljnost velikih gubitaka od nesreće za pojedine delatnosti kao što su opšta odgovornost, komercijalna vozila i naknade radnika.
• Količina vremena koju će korisnik na stimu provesti igrajući razne igre. (Neke igre se puno igraju, dok se većina njih skoro nikad ne igra.)
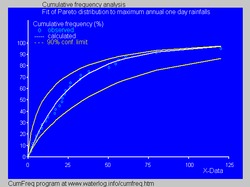
• U hidrologiji Paretova distribucija se koristi za ekstremne događaje kao što su godišnje maksimalne jednodnevne padavine i rečni ispusti. Plava slika ilustruje uklapanje Paretove distribucije u rangirane godišnje maksimume jednodnevnih padavina. Takođe je prikazan 90% pojas pouzdanosti baziran na binomnoj distribuciji. Podaci o padavinama su predstavljeni pomoću Q–Q grafika kao dela analize kumulativne frekvencije.

Literatura

• Шаблон:Cite journal
• Шаблон:Cite book

• Шаблон:Cite journal

• Шаблон:Cite journal

Spoljašnje veze

• Шаблон:Springer
• Шаблон:MathWorld
• Шаблон:Citation
• Шаблон:Cite conference
• -{syntraf1.c Шаблон:Wayback is a C program to generate synthetic packet traffic with bounded Pareto burst size and exponential interburst time.}-