Paraboloid

Parabolod

U geometriji, paraboloid je kvadratna površina koja ima tačno jednu osu simetrije i nema centar simetrije. Termin "paraboloid" izveden je od parabole, što se odnosi i na konusni presjek koji ima slično svojstvo simetrije.

Paraboloid je geometrijska površina koja nastaje rotacijom parabole po njenoj osi.

Paraboloid

Paraboloid je geometrijska površina drugog reda. Postoje dve vrste paraboloida: eliptični i hiperbolički.

Eliptični paraboloid

Eliptični paraboloid.

Eliptični paraboloid je telo čija je baza eliptičnog oblika i ima minimalnu ili maksimalnu tačku.

Algebarski model Eliptični paraboloid s vrhom u tački $[x_0,y_0,z_0]$ i ravni simetrije paralelnim s ravni $x=0$ i $y=0$ ima jednačinu: $z-z_0=\frac{{(x-x_0)}^2}{2p}+\frac{{(y-y_0)}^2}{2q}$

gde je $pq>0$

Rotacioni paraboloid

Rotacioni paraboloid je telo koje nastaje rotacijom parabole oko sopstvene ose i kruga koji čini bazu tela. Algebarski model Rotacioni paraboloid sa vrhom u tački $[x_0,y_0,z_0]$ je specijalan slučaj eliptičnog parabolida, za koji važi da je $p=q$, to znači za rotacioni paraboloid sa osom rotacije paralelnoj sa osom z važi: $2p(z-z_0)={(x-x_0)}^2+{(y-y_0)}^2$

Volumen rotacionog paraboloida: $V=\frac{1}{2}\pi {\rho }^{2}h$ gde je $\rho$ poluprečnik kružne baze i $h$ je visina paraboloida

Hiperbolički paraboloid

Hiperbolički paraboloid.

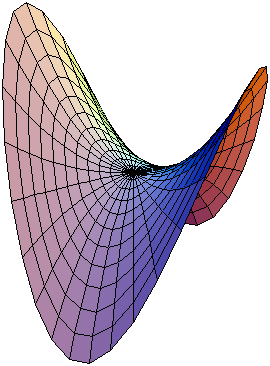
Algebarski model Hiperbolički paraboloid sa vrhom u tački $[x_0,y_0,z_0]$ i ravni simetrije paralelne sa ravni $x=0$ i $y=0$ ima jednačinu: $z-z_0=\frac{{(x-x_0)}^2}{2p}-\frac{{(y-y_0)}^2}{2q}$

gde je $pq>0$

Osobine

U oblasti hiperboličkog paraboloida postoje dva sistema pravih, pri čemu svaka prava jednog sistema preseca svaku pravu drugog sistema, ili proizvoljne dve prave jednog sistema se mimoilaze. Za paraboloid sa centrom u tački $[0,0,0]$ mogu se oba sistema pravih zapisati kao

$k_1(\frac{x}{\sqrt{2|p|}}+\frac{y}{\sqrt{2|q|}})=\frac{p}{|p|}{k}_{2}z$

$k_2(\frac{x}{\sqrt{2|p|}}-\frac{y}{\sqrt{2|q|}})=k_1$

$k_1(\frac{x}{\sqrt{2|p|}}-\frac{y}{\sqrt{2|q|}})=\frac{p}{|p|}{k}_{2}z$

$k_2(\frac{x}{\sqrt{2|p|}}+\frac{y}{\sqrt{2|q|}})=k_1$