Рекурзивни алгоритам најмањих квадрата

Рекурзивни алгоритам најмањих квадрата (RLS) је адаптивни филтер који рекурзивно утврђује коефицијенте који смањују пондерисани линеарни најмањи квадрат функција трошкова у вези улазних сигнала. Ово је за разлика у односу на друге алгоритме као што је алгоритам најмањих средњих квадрата (LMS) чији је циљ да смањи средње квадратне грешке. У извођење рекурзивног алгоритма најмањих квадрата, улазни сигнал се сматра детерминистичким, док се алгоритам најмањих средњих квадрата и слични алгоритми сматрају стохастичком. У поређењу са већином својих конкурената, експонати рекурзивног алгоритма најмањих квадрат изузетно брзо конвергирају. Међутим, ова корист долази по цену високог рачунарске комплексности.

Мотивација

RLS је открио Карл Фридрих Гаус али остаје неискоришћен или игнорисан до 1950. године, када Плацкет открива оригинални рад Гауса од 1821. У принципу, RLS алгоритми могу да се користе за решавање сваког проблема који могу да реше адаптивни филтери, На пример, претпоставимо да је сигнал d(n) који се преноси преко еха, бучни канал који узрокује да буде примљен као

$x(n)=\sum _{k=0}^q{b}_n(k)d(n-k)+v(n)$

где $v(n)$ представља додатну буку. Ми ћемо покушати да опоравимо жељени сигнал $d(n)$ употребом $p+1$-tap импулса коначних одзива, $𝐰$:

$\hat{d}(n)=\sum _{k=0}^p{w}_n(k)x(n-k)={𝐰}_n^{𝑇}{𝐱}_n$

где ${𝐱}_n=[x(n)x(n-1)\dots x(n-p){]}^T$ је вектор који садржи $p+1$ Најновији узорци $x(n)$. Наш циљ је да се процени параметре филтера $𝐰$, и у сваком тренутку n мислимо на нове најмањих квадрата процена ${𝐰}_n$. Како време пролази, желимо да се у потпуности избегну преправке алгоритма најмањих квадрата и да пронађу нову процену за ${𝐰}_{n+1}$, у смислу ${𝐰}_n$.

Корист од RLS алгоритма је да нема потребе обрнути матрицу, чиме се штеди рачунарска снага. Још једна предност је у томе што даје интуицију иза таквих резултата као Калман филтер.

Дискусија

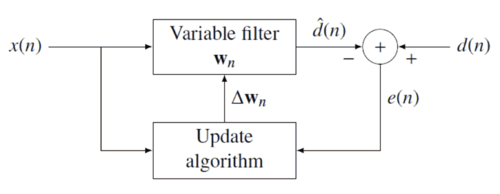
Идеја РЛС филтера је да минимизира функцију трошкова $C$ и адекватно одабира филтер коефицијенти ${𝐰}_n$, ажурирање филтера кад стигну нови подаци. Сигнал грешке $e(n)$ и жељени сигнал $d(n)$ су дефинисани у дијаграму негативне повратне спреге :

Грешка имплицитно зависи од коефицијента филтера путем процене. $\hat{d}(n)$:

$e(n)=d(n)-\hat{d}(n)$

Најмања функција квадрата грешка $C$— желимо да се цена функција минимизира-као функција e(n) стога такође зависи од коефицијента филтера: $C({𝐰}_n)=\sum _{i=0}^n{\lambda }^{n-i}{e}^2(i)$ где је $0<\lambda \le 1$ " фактор заборављања " који даје експоненцијално мању тежину старијим узорцима грешака.

Функција трошкова је сведена на минимум узимањем парцијалног извода за све ставке $k$ коефицијента вектора ${𝐰}_n$ и постављање резултата на нулу:$\frac{\partial C({𝐰}_n)}{\partial w_n(k)}=\sum _{i=0}^{n}2{\lambda }^{n-i}e(i)\frac{\partial e(i)}{\partial w_n(k)}=-\sum _{i=0}^{n}2{\lambda }^{n-i}e(i)x(i-k)=0k=0,1,\cdots ,p$ Даље, замени $e(n)$ са дефиницијом сигнала грешке

$\sum _{i=0}^n{\lambda }^{n-i}[d(i)-\sum _{l=0}^p{w}_n(l)x(i-l)]x(i-k)=0k=0,1,\cdots ,p$

Преуређивање једначине приноса

$\sum _{l=0}^p{w}_n(l)[\sum _{i=0}^n{\lambda }^{n-i}x(i-l)x(i-k)]=\sum _{i=0}^n{\lambda }^{n-i}d(i)x(i-k)k=0,1,\cdots ,p$

Овај облик може да се изрази у смислу матрице

${𝐑}_x(n){𝐰}_n={𝐫}_{dx}(n)$

where ${𝐑}_x(n)$ је измерен узорак коваријанси матрица за $x(n)$, и ${𝐫}_{dx}(n)$ је еквивалентна процена за попречну-коваријансу од $d(n)$ и $x(n)$ На основу овог израза налазимо коефицијенте који минимизирају трошкове функције као::${𝐰}_n={𝐑}_x^{-1}(n){𝐫}_{dx}(n)$ Ово је главни резултат дискусије.

Избор $\lambda$

Мањи $\lambda$ је, мали допринос претходним узорцима. То чини филтер више осетљивим на недавне узорке, што значи више флуктуације у филтеру коефицијента. За $\lambda =1$ случај се узима као пример растућег РЛС алгоритма. У пракси, $\lambda$ се обично бира између 0,98 и 1.

Рекурзивни алгоритам

Расправа је резултирала у једној једначини да се одреди коефицијент вектор који минимизира функцију трошкова. У овом одељку желимо да изведемо рекурзивно решење у облику

${𝐰}_n={𝐰}_{n-1}+\mathrm{\Delta }{𝐰}_{n-1}$

где $\mathrm{\Delta }{𝐰}_{n-1}$ је корективни фактор у времену $n-1$. Истражујемо порекло рекурзивног алгоритма изражавајући унакрсно коваријансу${𝐫}_{dx}(n)$ поводом ${𝐫}_{dx}(n-1)$

${𝐫}_{dx}(n)$	$=\sum _{i=0}^n{\lambda }^{n-i}d(i)𝐱(i)$
	$=\sum _{i=0}^{n-1}{\lambda }^{n-i}d(i)𝐱(i)+{\lambda }^{0}d(n)𝐱(n)$
	$=\lambda {𝐫}_{dx}(n-1)+d(n)𝐱(n)$

где је$𝐱(i)$$p+1$димензионални вектор података:$𝐱(i)=[x(i),x(i-1),\dots ,x(i-p){]}^T$ Слично изражавамо ${𝐑}_x(n)$ У погледу ${𝐑}_x(n-1)$ од

${𝐑}_x(n)$	$=\sum _{i=0}^n{\lambda }^{n-i}𝐱(i){𝐱}^T(i)$
	$=\lambda {𝐑}_x(n-1)+𝐱(n){𝐱}^T(n)$

Да би генерисали коефицијент вектора ми смо заинтересовани за супротност од детерминистичке матрице. Из тог задатка идентитет матрица долази у комбинацији. Са

$A$	$=\lambda {𝐑}_x(n-1)$ is $(p+1)$-by-$(p+1)$
$U$	$=𝐱(n)$ is $(p+1)$-by-1
$V$	$={𝐱}^T(n)$ is 1-by-$(p+1)$
$C$	$={𝐈}_1$ is the 1-by-1

Следи идентитет матрица

${𝐑}_x^{-1}(n)$	$=$	${[\lambda {𝐑}_x(n-1)+𝐱(n){𝐱}^T(n)]}^{-1}$
	$=$	${\lambda }^{-1}{𝐑}_x^{-1}(n-1)$
		$-{\lambda }^{-1}{𝐑}_x^{-1}(n-1)𝐱(n)$
		${\{1+{𝐱}^T(n){\lambda }^{-1}{𝐑}_x^{-1}(n-1)𝐱(n)\}}^{-1}{𝐱}^T(n){\lambda }^{-1}{𝐑}_x^{-1}(n-1)$

У складу са стандардном литературом, дефинишемо

$𝐏(n)$	$={𝐑}_x^{-1}(n)$
	$={\lambda }^{-1}𝐏(n-1)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)$

где је "добијен вектор"$g(n)$

$𝐠(n)$	$={\lambda }^{-1}𝐏(n-1)𝐱(n){\{1+{𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)\}}^{-1}$
	$=𝐏(n-1)𝐱(n){\{\lambda +{𝐱}^T(n)𝐏(n-1)𝐱(n)\}}^{-1}$

Пре него што кренемо даље, неопходно је да се донесе $𝐠(n)$ у другом облику

$𝐠(n)\{1+{𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)\}$	$={\lambda }^{-1}𝐏(n-1)𝐱(n)$
$𝐠(n)+𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)$	$={\lambda }^{-1}𝐏(n-1)𝐱(n)$

Одузимањем другог мандата на левој страни приноса

$𝐠(n)$	$={\lambda }^{-1}𝐏(n-1)𝐱(n)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)$
	$={\lambda }^{-1}[𝐏(n-1)-𝐠(n){𝐱}^T(n)𝐏(n-1)]𝐱(n)$

Са рекурзивном дефиницијом $𝐏(n)$ жељена форма прати

$𝐠(n)=𝐏(n)𝐱(n)$

Сада смо спремни да завршимо рекурзију. Као што је наведено

${𝐰}_n$	$=𝐏(n){𝐫}_{dx}(n)$
	$=\lambda 𝐏(n){𝐫}_{dx}(n-1)+d(n)𝐏(n)𝐱(n)$

Други корак произлази из рекурзивне дефиниције${𝐫}_{dx}(n)$. Затим смо уградили рекурзивно дефиниције $𝐏(n)$ заједно са алтернативним обликом $𝐠(n)$ и добијамо

${𝐰}_n$	$=\lambda [{\lambda }^{-1}𝐏(n-1)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)]{𝐫}_{dx}(n-1)+d(n)𝐠(n)$
	$=𝐏(n-1){𝐫}_{dx}(n-1)-𝐠(n){𝐱}^T(n)𝐏(n-1){𝐫}_{dx}(n-1)+d(n)𝐠(n)$
	$=𝐏(n-1){𝐫}_{dx}(n-1)+𝐠(n)[d(n)-{𝐱}^T(n)𝐏(n-1){𝐫}_{dx}(n-1)]$

Са${𝐰}_{n-1}=𝐏(n-1){𝐫}_{dx}(n-1)$ долазимо до једначине за ажурирање

${𝐰}_n$	$={𝐰}_{n-1}+𝐠(n)[d(n)-{𝐱}^T(n){𝐰}_{n-1}]$
	$={𝐰}_{n-1}+𝐠(n)\alpha (n)$

Где је $\alpha (n)=d(n)-{𝐱}^T(n){𝐰}_{n-1}$Грешка израчунавања "после" филтера се ажурира::$e(n)=d(n)-{𝐱}^T(n){𝐰}_n$ То значи да смо нашли фактор корекције:$\mathrm{\Delta }{𝐰}_{n-1}=𝐠(n)\alpha (n)$

Овај интуитивно задовољавајући резултат указује да је корективни фактор директно пропорционалан грешкама и појачањима вектора, и да контролише колика осетљивост се жели.

RLS алгоритам резиме

RLS алгоритам за pсе помоћу RLS филтера може сумирати на:

Параметри:	$p=$ поредак филтера
	$\lambda =$ фактор заборављања
	$\delta =$ вредност да се покрене $𝐏(0)$
Иницијализација:	$𝐰(n)=0$,
	$x(k)=0,k=-p,\dots ,-1$,
	$d(k)=0,k=-p,\dots ,-1$
	$𝐏(0)={\delta }^{-1}I$ где је $I$ матрица идентитета ранга $p+1$
Обрачун:	За $n=1,2,\dots$
	$𝐱(n)=\left[\begin{array}{c}x(n)\\ x(n-1)\\ ⋮\\ x(n-p)\end{array}\right]$
	$\alpha (n)=d(n)-{𝐱}^T(n)𝐰(n-1)$
	$𝐠(n)=𝐏(n-1){𝐱}^{*}(n){\{\lambda +{𝐱}^T(n)𝐏(n-1){𝐱}^{*}(n)\}}^{-1}$
	$𝐏(n)={\lambda }^{-1}𝐏(n-1)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)$
	$𝐰(n)=𝐰(n-1)+\alpha (n)𝐠(n)$.

Имајте на уму да рекурзија за $P$ следи алгебарска Рикатијева једначина и тако повлачи паралеле до Калман филтера.

Рекурзивне решетке најмањих квадрата филтера (LRLS)

Рекурзивне решетке најмањих квадрата филтера се односи на стандардни RLS, осим да је потребно мање аритметичких операција . Она нуди додатне предности у односу на конвенционалне LMS алгоритме као што су брже стопе конвергенције, модуларне структуре, и неосетљивост на варијацијама у ширења улазне корелационе матрице.LRLS алгоритам заснован је на грешкама и укључује нормализовани облик. Извођење је слична стандардном RLS алгоритму и заснива се на дефиницији $d(k)$. У предикционом случају, имамо $d(k)=x(k)$ са улазним сигналом $x(k-1)$ као највиши узорак. Предвиђање заосталих случајева $d(k)=x(k-i-1)$, где индекс узорка у прошлости желимо да предвидимо, а улазни сигнал $x(k)$ је најновији узорак.

Преглед параметара

${\kappa }_f(k,i)$ је напредни коефицијент рефлексије

${\kappa }_b(k,i)$ је назадан коефицијент рефлексије

$e_f(k,i)$ представља тренутно апостериори напредно предвиђање о грешци

$e_b(k,i)$ представља тренутно апостериори назадно предвиђање о грешци

${\xi }_{b_{min}}^d(k,i)$ је минимум најмањих квадрата назадно предвиђање грешака

${\xi }_{f_{min}}^d(k,i)$је минимум најмањих квадрата напредно предвиђање грешака

$\gamma (k,i)$ је фактор конверзије између априори и апостериори, грешке

$v_i(k)$ су вишеструки коефицијенти.

$ϵ$ је мала позитивна константа која може бити 0.01

LRLS преглед алгоритма

Алгоритам за LRLS филтер се може сажети у

Иницијализација:
	For i = 0,1,...,N
	Шаблон:Pad$\delta (-1,i)={\delta }_D(-1,i)=0$ (if x(k) = 0 for k < 0)
	Шаблон:Pad${\xi }_{b_{min}}^d(-1,i)={\xi }_{f_{min}}^d(-1,i)=ϵ$
	Шаблон:Pad$\gamma (-1,i)=1$
	Шаблон:Pad$e_b(-1,i)=0$
	End
Израчунавање:
	For k ≥ 0
	Шаблон:Pad$\gamma (k,0)=1$
	Шаблон:Pad$e_b(k,0)=e_f(k,0)=x(k)$
	Шаблон:Pad${\xi }_{b_{min}}^d(k,0)={\xi }_{f_{min}}^d(k,0)=x^2(k)+\lambda {\xi }_{f_{min}}^d(k-1,0)$
	Шаблон:Pad$e(k,0)=d(k)$
	Шаблон:PadFor i = 0,1,...,N
	Шаблон:Pad$\delta (k,i)=\lambda \delta (k-1,i)+\frac{e_b(k-1,i)e_f(k,i)}{\gamma (k-1,i)}$
	Шаблон:Pad$\gamma (k,i+1)=\gamma (k,i)-\frac{e_b^2(k,i)}{{\xi }_{b_{min}}^d(k,i)}$
	Шаблон:Pad${\kappa }_b(k,i)=\frac{\delta (k,i)}{{\xi }_{f_{min}}^d(k,i)}$
	Шаблон:Pad${\kappa }_f(k,i)=\frac{\delta (k,i)}{{\xi }_{b_{min}}^d(k-1,i)}$
	Шаблон:Pad$e_b(k,i+1)=e_b(k-1,i)-{\kappa }_b(k,i)e_f(k,i)$
	Шаблон:Pad$e_f(k,i+1)=e_f(k,i)-{\kappa }_f(k,i)e_b(k-1,i)$
	Шаблон:Pad${\xi }_{b_{min}}^d(k,i+1)={\xi }_{b_{min}}^d(k-1,i)-\delta (k,i){\kappa }_b(k,i)$
	Шаблон:Pad${\xi }_{f_{min}}^d(k,i+1)={\xi }_{f_{min}}^d(k,i)-\delta (k,i){\kappa }_f(k,i)$
	Шаблон:Pad
	Шаблон:Pad${\delta }_D(k,i)=\lambda {\delta }_D(k-1,i)+\frac{e(k,i)e_b(k,i)}{\gamma (k,i)}$
	Шаблон:Pad$v_i(k)=\frac{{\delta }_D(k,i)}{{\xi }_{b_{min}}^d(k,i)}$
	Шаблон:Pad$e(k,i+1)=e(k,i)-v_i(k)e_b(k,i)$
	Шаблон:PadEnd
	End

Нормализован рекурзиван филтер најмањих квадрата (NLRLS)

Нормализована форма LRLS има мање рекурзије и променљивих. Може се израчунати применом нормализације интерних варијабли алгоритма који ће задржати своју величину. Ово се углавном не користи у реалном времену апликације због броја одељења и квадратног корена операција која долази са високим рачунарским оптерећењем.

NLRLS преглед алгоритма

Алгоритам за NLRLS филтер се може сажети у

Иницијализација:
	For i = 0,1,...,N
	Шаблон:Pad$\bar{\delta }(-1,i)=0$ (if x(k) = d(k) = 0 for k < 0)
	Шаблон:Pad${\bar{\delta }}_D(-1,i)=0$
	Шаблон:Pad${\bar{e}}_b(-1,i)=0$
	End
	Шаблон:Pad${\sigma }_x^2(-1)=\lambda {\sigma }_d^2(-1)=ϵ$
Израчунавање:
	For k ≥ 0
	Шаблон:Pad${\sigma }_x^2(k)=\lambda {\sigma }_x^2(k-1)+x^2(k)$ (улазни сигнал снаге)
	Шаблон:Pad${\sigma }_d^2(k)=\lambda {\sigma }_d^2(k-1)+d^2(k)$ (референтни сигнал снаге)
	Шаблон:Pad${\bar{e}}_b(k,0)={\bar{e}}_f(k,0)=\frac{x(k)}{{\sigma }_x(k)}$
	Шаблон:Pad$\bar{e}(k,0)=\frac{d(k)}{{\sigma }_d(k)}$
	Шаблон:Pad For i = 0,1,...,N
	Шаблон:Pad$\bar{\delta }(k,i)=\delta (k-1,i)\sqrt{(1-{\bar{e}}_b^2(k-1,i))(1-{\bar{e}}_f^2(k,i))}+{\bar{e}}_b(k-1,i){\bar{e}}_f(k,i)$
	Шаблон:Pad${\bar{e}}_b(k,i+1)=\frac{{\bar{e}}_b(k-1,i)-\bar{\delta }(k,i){\bar{e}}_f(k,i)}{\sqrt{(1-\stackrel{2}{\stackrel{‾}{\delta }}(k,i))(1-{\bar{e}}_f^2(k,i))}}$
	Шаблон:Pad${\bar{e}}_f(k,i+1)=\frac{{\bar{e}}_f(k,i)-\bar{\delta }(k,i){\bar{e}}_b(k-1,i)}{\sqrt{(1-\stackrel{2}{\stackrel{‾}{\delta }}(k,i))(1-{\bar{e}}_b^2(k-1,i))}}$
	Шаблон:Pad
	Шаблон:Pad${\bar{\delta }}_D(k,i)={\bar{\delta }}_D(k-1,i)\sqrt{(1-{\bar{e}}_b^2(k,i))(1-\stackrel{2}{\stackrel{‾}{e}}(k,i))}+\bar{e}(k,i){\bar{e}}_b(k,i)$
	Шаблон:Pad$\bar{e}(k,i+1)=\frac{1}{\sqrt{(1-{\bar{e}}_b^2(k,i))(1-{\bar{\delta }}_D^2(k,i))}}[\bar{e}(k,i)-{\bar{\delta }}_D(k,i){\bar{e}}_b(k,i)]$
	Шаблон:PadEnd
	End

Литература

• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• Шаблон:Cite book
• R.L.Plackett, Some Theorems in Least Squares, Biometrika, 1950, 37, 149-157, Шаблон:ISSN
• C.F.Gauss, Theoria combinationis observationum erroribus minimis obnoxiae, 1821, Werke, 4. Gottinge