Математичко клатно

Математичко клатно је осцилаторни систем који се састоји из неистегљиве нити занемарљиве масе на коју је обешена куглица занемарљиво малих димензија у односу на дужину нити и знатно веће масе од масе нити и који може да осцилује под утицајем Земљине теже.

Период осциловања

Преко тригонометријских односа и уз помоћ разлагања сила, других математичких веза, као и преко закона одржања енергије може се извести образац за период осциловања математичког клатна при малим угловима амплитудног отклона.

Први начин извођења

На слици је приказано клатно отклоњено од равнотежног положаја и на њој су обележене основне величине које описују кретање клатна. Веза између ових физичких величина је описана диференцијалном једначином:

$\frac{d^2\theta }{d{t}^2}+\frac{g}{\ell }\sin \theta =0$

Даљим сређивањем:

$\frac{d\theta }{dt}=\sqrt{\frac{2g}{\ell }(\cos \theta -\cos {\theta }_0)}$

За мале углове важи следећа апроксимација:

$\sin \theta \approx \theta$

одакле се даљим рачуном и поједностављењем добија:

$T=2\pi \sqrt{\frac{\ell }{g}}$

Овај израз описује да је период осцилације математичког клатна сразмеран квадратном корену дужине клатна. Из овог израза следи да се познавањем дужине клатна и периода осциловања може одредити колико износи убрзање земљине теже.

Други начин

Ово је нешто једноставнији начин извођења претходне формуле.

Силу mg можемо разложити на две компоненте: $mg\sin \theta$ и $mg\cos \theta$. Да би систем хармонијски осциловао потребно је дејство повратне силе облика -kx. Изједначавањем налазимо: $mg\sin \theta =kx$. Пошто је за мале углове:

$\sin \theta =\frac{x}{l}$

Следи:

$\frac{mgx}{l}=kx$

Одатле добијамо да је:

$mg=kl$

$\frac{m}{k}=\frac{l}{g}$

Упоређивањем са формулом за период осциловања хармонијског хармонијског осцилатора добијамо образац:

$T=2\pi \sqrt{\frac{\ell }{g}}$

Анимација која приказује вектор брзине(V) и убрзања(А)

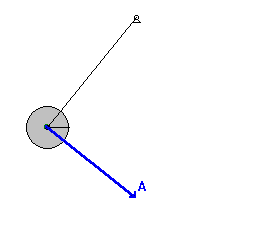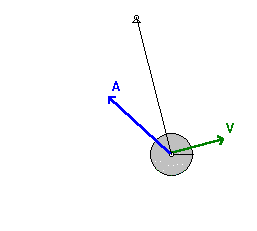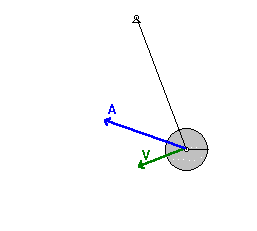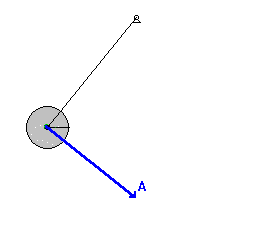
Математичко клатно као хармонијски осцилатор

Математичко клатно је хармонијски осцилатор, сагласно претпоставци искоришћеној у претходном доказу, али само за мале углове када важи апроксимација са синусом угла, која је у њему споменута. Међутим чак и са нешто већим угловима(до око 8°) претходно изведена формула даје приближно тачне резултате(при чему са порастом угла та тачност опада). Ипак за прецизнија мерења не може се увек користити(већ само за јако мале углове) и за то постоји сложено извођење које узима у обзир ограничен опсег важења те апроксимације и даје тачну вредност периода осциловања у посматраном систему.

Физичко клатно

Математичко клатно је облик идеализације. Физичко клатно представља произвољно круто тело које под утицајем Земљине теже може осциловати око хоризонталне осе која не пролази кроз његово средиште. Kao специјалан случај физичког клатна, када важи I=ml², где је I момент инерције јавља се математичко клатно. С тим у вези се користимо појам редуковане дужине математичког клатна.

Додатна литература

• Шаблон:Cite book
• Шаблон:Cite journal
• Шаблон:Cite journal

Спољашње везе

• Pendulum Шаблон:En