Датотека:Em old faithful.gif
Извор: testwiki
Пређи на навигацију
Пређи на претрагу
Em_old_faithful.gif (360 × 360 пиксела, величина датотеке: 272 kB, MIME тип: image/gif, петља, 30 кадрова, 6,0 с)
Ова датотека се налази на Викимедијина остава и може да се користи на другим пројектима. Њен опис је приказан испод.
Опис
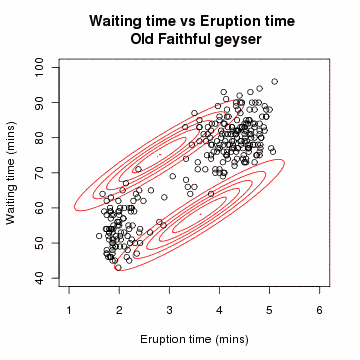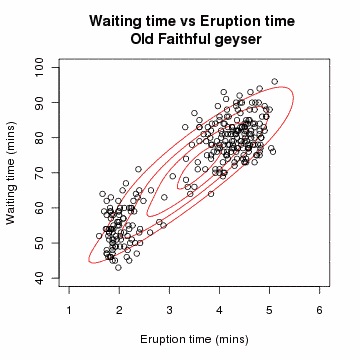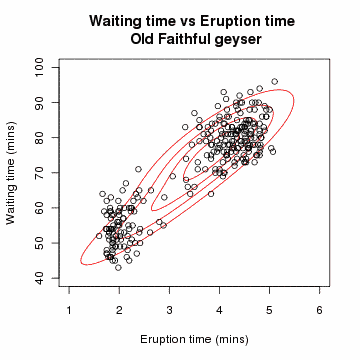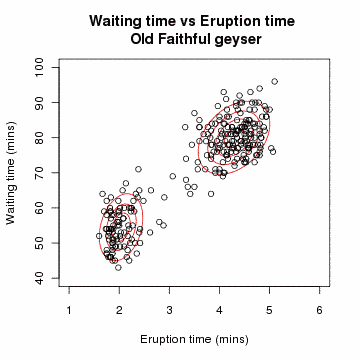
| ОписEm old faithful.gif | An animation of the EM algorithm to a 2 component Gaussian mixture model on the Old Faithful dataset |
| Датум | |
| Извор | Сопствено дело |
| Аутор | 3mta3 (talk) 16:55, 23 March 2009 (UTC) |
Created in R with code below (released under same license as image), combined into animated gif using ImageMagick.
There should be a way to make this file smaller (e.g. using less colours or an animated PNG). If you can, feel free to upload a new copy.
#load library for multivariate normal
library(mvtnorm)
#load Old Faithful data frame
data(faithful)
#setup grid for plotting
xpts <- seq(from=1,to=6,length.out=100)
ypts <- seq(from=40,to=100,length.out=100)
#initial parameter estimates (chosen to be deliberately bad)
theta <- list(
tau=c(0.5,0.5),
mu1=c(2.8,75),
mu2=c(3.6,58),
sigma1=matrix(c(0.8,7,7,70),ncol=2),
sigma2=matrix(c(0.8,7,7,70),ncol=2)
)
#E step: calculates conditional probabilities for latent variables
E.step <- function(theta)
t(apply(cbind(
theta$tau[1] * dmvnorm(faithful,mean=theta$mu1,sigma=theta$sigma1),
theta$tau[2] * dmvnorm(faithful,mean=theta$mu2,sigma=theta$sigma2)
),1,function(x) x/sum(x)))
#M step: calculates the parameter estimates which maximise Q
M.step <- function(T) list(
tau= apply(T,2,mean),
mu1= apply(faithful,2,weighted.mean,T[,1]),
mu2= apply(faithful,2,weighted.mean,T[,2]),
sigma1= cov.wt(faithful,T[,1])$cov,
sigma2= cov.wt(faithful,T[,2])$cov)
#function to plot current data
plot.em <- function(theta){
mixture.contour <- outer(xpts,ypts,function(x,y) {
theta$tau[1]*dmvnorm(cbind(x,y),mean=theta$mu1,sigma=theta$sigma1) + theta$tau[2]*dmvnorm(cbind(x,y),mean=theta$mu2,sigma=theta$sigma2)
})
contour(xpts,ypts,mixture.contour,nlevels=5,drawlabel=FALSE,col="red",xlab="Eruption time (mins)",ylab="Waiting time (mins)",main="Waiting time vs Eruption time of the Old Faithful geyser")
points(faithful)
}
#plot initial contours
iter <- 1
png(filename=paste("em",formatC(iter,width=4,flag="0"),".png",sep=""))
plot.em(theta)
dev.off()
#run EM and plot
for (iter in 2:30){
T <- E.step(theta)
theta <- M.step(T)
png(filename=paste("em",formatC(iter,width=4,flag="0"),".png",sep=""))
plot.em(theta)
dev.off()
}
Лиценцирање
Ја, носилац ауторских права над овим делом, објављујем исто под следећим лиценцама:
Ова датотека је доступна под лиценцом Creative Commons Ауторство-Делити под истим условима 3.0 Unported.
- Дозвољено је:
- да делите – да умножавате, расподељујете и преносите дело
- да прерађујете – да прерадите дело
- Под следећим условима:
- ауторство – Морате да дате одговарајуће заслуге, обезбедите везу ка лиценци и назначите да ли су измене направљене. Можете то урадити на било који разуман манир, али не на начин који предлаже да лиценцатор одобрава вас или ваше коришћење.
- делити под истим условима – Ако измените, преобразите или доградите овај материјал, морате поделити своје доприносе под истом или компатибилном лиценцом као оригинал.

|
Дата је дозвола да се копира, дистрибуира и/или мења овај документ под условима ГНУ-ове лиценце за слободну документацију, верзије 1.2 или било које новије верзије коју објави Задужбина за слободни софтвер; без непроменљивих одељака и без текста на насловној и задњој страни. Текст лиценце можете прочитати овде.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
Изаберите лиценцу по жељи.
Поднаписи
Укратко шта ова датотека представља/приказује
Ставке приказане у овој датотеци
приказује
неке вредности
23. март 2009
Историја датотеке
Кликните на датум/време да бисте видели тадашњу верзију датотеке.
| Датум/време | Минијатура | Димензије | Корисник | Коментар | |
|---|---|---|---|---|---|
| тренутна | 18:10, 23. март 2009. | 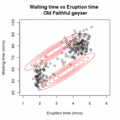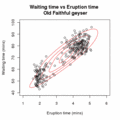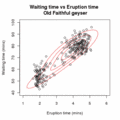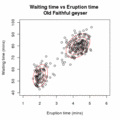 | 360 × 360 (272 kB) | wikimediacommons>3mta3 | A bit smaller |
Употреба датотеке
Следећа страница користи ову датотеку: