Konveksni skup

Ilustracija konveksnog skupa koji izgleda donekle poput deformisanog kruga. Crni linijski segment koji povezuje tačke x i kompletno leži unutar (zelenog) skupa. Budući da je to tačno za bilo koje tačke x i y unutar skupa koje se mogu izabrati, skup je konveksan.

Ilustracija nekonveksnog skupa. Kako (crveni) deo (crngo i crvenog) linijskog-segmenta koji povezuje tačke x i y leži izvan (zelenog) skupa, skup je nekonveksan.

U geometriji, podskup Euklidovog prostora, ili specifičnije afini prostor nad realnim brojevima, je konveksan ako, sa bilo koje dve tačke, on povezuje ceo linijski segment koji ih povezuje. Ekvivalentno, konveksni skup ili konveksni region je podskup koji preseca svaku liniju u jednom linijskom segmentu (verovatno praznom). Na primer, čvrsta kocka je konveksni skup, dok sve što je šuplje ili ima udubljenje, na primer, oblik polumeseca, nije konveksno.

Granica konveksnog skupa je uvek konveksna kriva. Presek svih konveksnih skupova koji sadrže dati podskup Шаблон:Mvar Euklidovog prostora naziva se konveksni omotač Шаблон:Mvar. To je najmanji konveksni skup koji sadrži Шаблон:Mvar.

Konveksna funkcija je realno vrednosna funkcija definisana na intervalu sa svojstvom da je njegov epigraf (skup tačaka na ili iznad grafikona funkcije) konveksni skup. Konveksna minimizacija je potpolje optimizacije koje izučava problem minimizacije konveksnih funkcija nad konveksnim skupovima. Prva grana matemakia posvećena izučavanju svojstava konveksnih skupova i konveksnih funkcija se naziva konveksna analiza.

Pojam konveksnog skupa može se generalizovati, kao što je opisano u daljem tekstu.

Definicije

Funkcija je konveksna, ako i samo ako njen epigraf, region (obojen zeleno) iznad njenog grafikona (prikazan plavom linijuom), je konveksan set.

Neka je Шаблон:Mvar vektorski prostor ili afini prostor nad realnim brojevima, ili, generalnije, nad nekim uređenim poljem. Ovim su obuhvaćeni Euklidovi prostori, koji su afini prostori. podskup Шаблон:Mvar od Шаблон:Mvar je konveksan ako je za svako Шаблон:Mvar i Шаблон:Mvar u Шаблон:Mvar, linijski segment koji povezuje Шаблон:Mvar i Шаблон:Mvar uključen u Шаблон:Mvar. To znači da afina kombinacija Шаблон:Math pripada Шаблон:Mvar, za svako Шаблон:Mvar i Шаблон:Mvar u Шаблон:Mvar, i Шаблон:Mvar na intervalu Шаблон:Math. To podrazumeva da je konveksnost (svojstvo da je konveksan) invarijantna pod afinim trasformacijama. Time se isto tako podrazumeva da je konveksni skup u realnom ili kompleksnom topološkom vektorskom prostoru povezan putanjom, i stoga povezan.

Skup Шаблон:Mvar je striktno konveksan ako je svaka tačka na linijskom segmentu koji povezuje Шаблон:Mvar i Шаблон:Mvar izuzev krajnjih tačaka u unutrašnjosti Шаблон:Mvar.

Skup Шаблон:Mvar je apsolutno konveksan ako je konveksan i balansiran.

Konveksni podskupovi iz Шаблон:Math (skupa realnih brojeva) su intervali i tačke iz Шаблон:Math. Neki primeri konveksnih podskupova Euklidske ravni su čvrsti pravilni mnogouglovi, čvrsti trouglovi i preseci čvrstih trouglova. Neki primeri konveksnih podskupova Euklidskog trodimenzionalnog prostora su Arhimedova tela i pravilni poliedri. Poliedri Kepler-Puansoa su primeri nekonveksnih skupova.

Nekonveksni skup

Skup koji nije koveksan se naziva nekonveksni skup. Mnogougao koji nije konveksni poligon se ponekad naziva konkavni poligon, a neki izvori generalnije koriste termin konkavni skup sa značenjem nekonveksni skup, mada ta upotreba većinom nije dozvoljena.

Komplement konveksnog skupa, kao što je epigraf konkavne funkcije, se ponekad naziva reverzni konveksni skup, posebno u kontekstu matematičke optimizacije.

Svojstva

Neka je dato Шаблон:Mvar tačaka Шаблон:Math u konveksnom skupu Шаблон:Mvar, i Шаблон:Mvar nenegativnih brojeva Шаблон:Math takvih da je Шаблон:Math, afina kombinacija $$\sum _{k=1}^r{\lambda }_k{u}_k$$ pripada Шаблон:Mvar. Kako je definicija konveksnog skupa slučaj Шаблон:Math, ovo svojstvo karakteriše konveksne skupove.

Takva afina kombinacija naziva se konveksna kombinacija Шаблон:Math.

Preseci i unije

Kolekcija konveksnih podskupova vektorskog prostora, afinog prostora ili euklidskog prostora ima sledeća svojstva:

1. Prazan skup i ceo prostor su konveksni.
2. Presek bilo koje kolekcije konveksnih skupova je konveksan.
3. Unija niza konveksnih skupova je konveksna, ako oni čine neopadajući lanac za uključivanje. Za ovo svojstvo, ograničenje na lance je važno, pošto unija dva konveksna skupa ne mora biti konveksna.

Zatvoreni konveksni skupovi

Zatvoreni konveksni skupovi su konveksni skupovi koji sadrže sve svoje granične tačke. Mogu se okarakterisati kao preseci zatvorenih poluprostora (skupovi tačaka u prostoru koje leže na jednoj strani hiperravni).

Iz ovoga što je upravo rečeno jasno je da su takvi preseci konveksni, a biće i zatvoreni skupovi. Da bi se dokazalo obrnuto, tj. da se svaki zatvoreni konveksni skup može predstaviti kao takav presek, potrebna je prateća teorema o hiperravni u obliku da za dati zatvoreni konveksni skup Шаблон:Mvar i tačku Шаблон:Mvar van njega postoji zatvoreni poluprostor Шаблон:Mvar koji sadrži Шаблон:Mvar a ne Шаблон:Mvar. Prateća teorema o hiperravni je poseban slučaj Han–Banahove teoreme funkcionalne analize.

Konveksni skupovi i pravougaonici

Neka je Шаблон:Mvar konveksno telo u ravni (konveksan skup čija unutrašnjost nije prazna). Može se upisati pravougaonik r u Шаблон:Mvar tako da je homotetička kopija R od r opisana oko Шаблон:Mvar. Pozitivni odnos homotetije je najviše 2 i: $$\frac{1}{2}\cdot \mathrm{Area}(R)\le \mathrm{Area}(C)\le 2\cdot \mathrm{Area}(r)$$

Blački-Santalo dijagrami

Skup svih ravnih konveksnih tela može se parametrizovati u smislu prečnika konveksnog tela D, njegovog radijusa r (najveći krug koji se nalazi u konveksnom telu) i njegov radijus kruga R (najmanji krug koji sadrži konveksno telo). Zapravo, ovaj skup se može opisati skupom nejednakosti koje daje $$2r\le D\le 2R$$ $$R\le \frac{\sqrt{3}}{3}D$$ $$r+R\le D$$ $$D^2\sqrt{4R^2-D^2}\le 2R(2R+\sqrt{4R^2-D^2})$$ i može se vizualizovati kao slika funkcije g koja preslikava konveksno telo u tačku Шаблон:Math datu sa (r/R, D/2R). Slika ove funkcije je poznata (r, D, R) Blački-Santalov dijagram.

Blački-Santalov (r, D, R) dijagram za planarna konveksna tela. $𝕃$ označava segment linije, ${𝕀}_{\frac{\pi }{3}}$ jednakostranični trougao, $ℝ𝕋$ Reloov trougao i ${𝔹}_2$ jedinični krug.

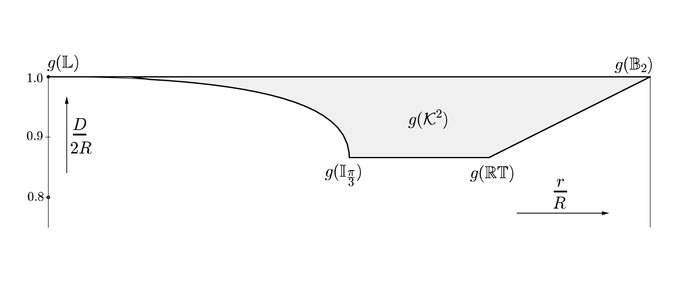
Alternativno, skup ${𝒦}^2$ takođe može biti parametrizovan njegovom širinom (najmanja udaljenost između bilo koje dve različite paralelne hiperravni), perimetrom i površinom.

Ostala svojstva

Neka je X topološki vektorski prostor i neka je $C\subseteq X$ konveksan.

• $\mathrm{Cl}C$ i $\mathrm{Int}C$ su oba konveksna (tj. zatvaranje i unutrašnjost konveksnih skupova su konveksni).
• Ako je $a\in \mathrm{Int}C$ i $b\in \mathrm{Cl}C$ onda je $[a,b[\subseteq \mathrm{Int}C$ (gde je $[a,b[:=\{(1-r)a+rb:0\le r<1\}$).
• Ako je $\mathrm{Int}C\ne \mathrm{\varnothing }$ onda je:
  • $\mathrm{cl}(\mathrm{Int}C)=\mathrm{Cl}C$, i
  • $\mathrm{Int}C=\mathrm{Int}(\mathrm{Cl}C)=C^i$, gde je $C^i$ algebarska unutrašnjost C.

Konveksni omotači i Minkovskijeve sume

Konveksni omotači

Svaki podskup Шаблон:Mvar vektorskog prostora je sadržan u najmanjem konveksnom skupu (koji se naziva konveksna ljuska Шаблон:Mvar), odnosno preseku svih konveksnih skupova koji sadrže Шаблон:Mvar. Operator konveksne ljuske Conv() ima karakteristična svojstva operatora ljuske:

• opširna: S ⊆ Conv(S),
• neopadajuća: Шаблон:Math implicira da je Шаблон:Math, i
• idempotentna: Шаблон:Math.

Operacija konveksne ljuske je potrebna da bi skup konveksnih skupova formirao rešetku, u kojoj je operacija „spajanja“ konveksni omotač unije dva konveksna skupa $$\mathrm{Conv}(S)\vee \mathrm{Conv}(T)=\mathrm{Conv}(S\cup T)=\mathrm{Conv}(\mathrm{Conv}(S)\cup \mathrm{Conv}(T)).$$ Presek bilo koje kolekcije konveksnih skupova je sam po sebi konveksan, tako da konveksni podskupovi (realnog ili kompleksnog) vektorskog prostora formiraju kompletnu rešetku.

Sabiranje Minkovskog

Minkovskijevo dodavanje skupova. Zbir kvadrata Q₁=[0,1]² i Q₂=[1,2]² je kvadrat Q₁+Q₂=[1,3]².

U realnom vektorskom prostoru, Minkovskijev zbir dva (neprazna) skupa, Шаблон:Math i Шаблон:Math, je definisan kao skup Шаблон:Math formiran dodavanjem vektora po elementima iz skupova sabiraka $$S_1+S_2=\{x_1+x_2:x_1\in S_1,x_2\in S_2\}.$$ Uopštenije, zbir Minkovskog konačne porodice (nepraznih) skupova Шаблон:Math je skup formiran sabiranjem vektora po elementima $$\sum _n{S}_n=\{\sum _n{x}_n:x_n\in S_n\}.$$

Za sabiranje Minkovskog, nulti skup Шаблон:Math koji sadrži samo nulti vektor Шаблон:Math ima posebnu važnost: Za svaki neprazan podskup S vektorskog prostora $$S+\{0\}=S;$$ u algebarskoj terminologiji, Шаблон:Math je element identiteta Minkovskijevog sabiranja (na kolekciji nepraznih skupova).

Konveksni ljuske Minkovskih suma

Minkovskijevo dodavanje se dobro ponaša u odnosu na operaciju uzimanja konveksnih ljuski, kao što pokazuje sledeći predlog:

Neka su Шаблон:Math podskupovi realnog vektorskog prostora, konveksni omotač njihovog Minkovskijevog zbira je zbir njihovih konveksnih omotača $$\mathrm{Conv}(S_1+S_2)=\mathrm{Conv}(S_1)+\mathrm{Conv}(S_2).$$

Ovaj rezultat važi uopštenije za svaku konačnu kolekciju nepraznih skupova: $$\text{Conv}\left(\sum _n{S}_n\right)=\sum _n\text{Conv}\left(S_n\right).$$

U matematičkoj terminologiji, operacije Minkovskijevogog sabiranja i formiranja konveksnih ljuski su komutativne operacije.

Minkovskijeva suma konveksnih skupova

Zbir Minkovskog dva kompaktna konveksna skupa je kompaktan. Zbir kompaktnog konveksnog skupa i zatvorenog konveksnog skupa je zatvoren.

Sledeća poznata teorema, koju je dokazao Diudoni 1966. godine, daje dovoljan uslov da razlika dva zatvorena konveksna podskupa bude zatvorena. Ona koristi koncept recesionog konusa nepraznog konveksnog podskupa S, definisanog kao: $$\mathrm{rec}S=\{x\in X:x+S\subseteq S\},$$ gde je ovaj skup konveksan konus koji sadrži $0\in X$ i zadovoljava $S+\mathrm{rec}S=S$. Treba imati na umu da ako je S zatvoren i konveksan onda je $\mathrm{rec}S$ zatvoren i za svako $s_0\in S$, $$\mathrm{rec}S=\bigcap _{t>0}t(S-s_0).$$

Teorema (Diudoni). Neka su A i B neprazni, zatvoreni i konveksni podskupovi lokalno konveksnog topološkog vektorskog prostora takvog da je $\mathrm{rec}A\cap \mathrm{rec}B$ linearni podprostor. Ako je A ili B lokalno kompaktan onda je A − B zatvoren.

Generalizacije i proširenja za konveksnost

Pojam konveksnosti u euklidskom prostoru može se generalizovati modifikacijom definicije u nekim ili drugim aspektima. Koristi se uobičajeni naziv „generalizovana konveksnost“, jer rezultujući objekti zadržavaju određena svojstva konveksnih skupova.

Zvezdasto-konveksni (zvezdasti) skupovi

Neka je Шаблон:Mvar skup u realnom ili kompleksnom vektorskom prostoru. Шаблон:Mvar je zvezdasto konveksan (u obliku zvezde) ako postoji Шаблон:Math u Шаблон:Mvar tako da je segment linije od Шаблон:Math do bilo koje tačke Шаблон:Mvar u Шаблон:Mvar sadržan u Шаблон:Mvar. Otuda je neprazan konveksan skup uvek zvezdasto konveksan, ali zvezdsto konveksni skup nije uvek konveksan.

Ortogonalna konveksnost

Primer generalizovane konveksnosti je ortogonalna konveksnost.

Skup Шаблон:Mvar u euklidskom prostoru naziva se ortogonalno konveksan ili orto-konveksan, ako bilo koji segment paralelan bilo kojoj od koordinatnih ose koje spajaju dve tačke od Шаблон:Mvar leži potpuno unutar Шаблон:Mvar. Lako je dokazati da je presek bilo koje kolekcije ortokonveksnih skupova ortokonveksan. Važe i neka druga svojstva konveksnih skupova.

Neeuklidska geometrija

Definicija konveksnog skupa i konveksnog omotača prirodno se proširuje na geometrije koje nisu euklidske definisanjem geodetski konveksnog skupa kao skupa koji sadrži geodetske koje spajaju bilo koje dve tačke u skupu.

Topologija reda

Konveksnost se može proširiti za potpuno uređen skup Шаблон:Mvar koji ima topologiju poretka.

Neka je Шаблон:Math. Potprostor Шаблон:Mvar je konveksan skup ako je za svaki par tačaka Шаблон:Math u Шаблон:Mvar takav da je Шаблон:Math, interval Шаблон:Math sadržan u Шаблон:Mvar. To jest, Шаблон:Mvar je konveksan ako i samo ako za svako Шаблон:Math u Шаблон:Mvar, Шаблон:Math implicira Шаблон:Math.

Konveksan skup generalno nije povezan: kontra-primer je dat podprostorom {1,2,3} u Шаблон:Math, koji je i konveksan i nije povezan.

Prostori konveksnosti

Pojam konveksnosti se može generalizovati na druge objekte, ako se kao aksiome izaberu određena svojstva konveksnosti.

Za dati skup Шаблон:Mvar, konveksnost nad Шаблон:Mvar je kolekcija Шаблон:Math podskupova Шаблон:Mvar koja zadovoljava sledeće aksiome:

1. Prazan skup i Шаблон:Mvar su u Шаблон:Math
2. Presek bilo koje kolekcije iz Шаблон:Math je u Шаблон:Math.
3. Unija lanca (u pogledu inkluzivne relacije) elemenata od Шаблон:Math je u Шаблон:Math.

Elementi Шаблон:Math se nazivaju konveksni skupovi, a par Шаблон:Math se naziva prostor konveksnosti. Za običnu konveksnost važe prve dve aksiome, a treća je trivijalna.

Za alternativnu definiciju apstraktne konveksnosti, koja je pogodnija za diskretnu geometriju, pogledajte konveksne geometrije povezane sa antimatroidima.

Konveksni prostori

Konveksnost se može generalizovati kao apstraktna algebarska struktura: prostor je konveksan ako je moguće uzeti konveksne kombinacije tačaka.

Literatura

• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation
• Шаблон:Citation

Spoljašnje veze

• Шаблон:Springer
• -{Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.}-